题目内容
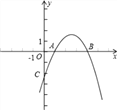
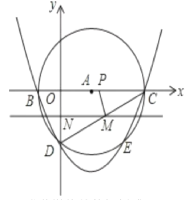
【题目】已知一次函数![]() 的图象与二次函数
的图象与二次函数![]() (
(![]() 为常数)的图象交于
为常数)的图象交于![]() 两点,且点
两点,且点![]() 的坐标为
的坐标为![]() .
.
(1)求出![]() 的值及点
的值及点![]() 的坐标;
的坐标;
(2)设![]() ,若
,若![]() 时,
时,![]() 随着
随着![]() 的增大而增大,且
的增大而增大,且![]() 也随着
也随着![]() 的增大而增大,求
的增大而增大,求![]() 的最小值和
的最小值和![]() 的最大值.
的最大值.
【答案】(1)![]() ,
,![]() 点坐标
点坐标![]() ;(2)
;(2)![]() ,
,![]() .
.
【解析】
(1)把A(0,3)代入![]() 和
和![]() 中可求得a、b的值,列方程组,解出即可得出点B的坐标;
中可求得a、b的值,列方程组,解出即可得出点B的坐标;
(2)分别求出两函数s、t的解析式,并配方成顶点式,写出当s 随着x 的增大而增大,且t 也随着x 的增大而增大的x的取值,与n≤x≤m相对应得出结论
(1)将![]() 代入
代入![]() ,得
,得![]()
则一次函数![]() ①
①
将![]() 代入
代入![]() ,得
,得![]()
∴二次函数![]() ②
②
联立①②

综上所述:![]() ,
,![]() 点坐标
点坐标![]()
(2)由(1)知![]() ,
,![]()
则![]()
![]()
∵![]() 随
随 ![]() 增大而增大,
增大而增大, ![]() 对称轴
对称轴 ![]() ,∴取
,∴取![]()
∵ ![]() 随
随 ![]() 增大而增大,
增大而增大,![]() 对称轴
对称轴 ![]() ,∴取
,∴取 ![]()
∵![]() ,
,![]()
∴![]() ,
,![]()

练习册系列答案
相关题目