题目内容
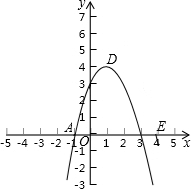 已知:如图,抛物线y=-x2+bx+c与x轴,y轴分别相交于点A(-1,0),B(0,3)两点,其顶点为D.
已知:如图,抛物线y=-x2+bx+c与x轴,y轴分别相交于点A(-1,0),B(0,3)两点,其顶点为D.(1)求该抛物线的解析式;
(2)若该抛物线与x轴的另一个交点为E.求四边形ABDE的面积;
(3)△AOB与△BDE是否相似?如果相似,请予以证明;如果不相似,请说明理由.
分析:(1)利用待定系数法将A(-1,0),B(0,3)两点代入解析式求出即可;
(2)根据二次函数的对称性即可得出E点坐标,利用四边形ABDE的面积=S△ABO+S梯形BOFD+S△DFE,求出即可;
(3)利用勾股定理求出BD,BE,DE,得出△BDE是直角三角形,再利用
=
=
,得出答案即可.
(2)根据二次函数的对称性即可得出E点坐标,利用四边形ABDE的面积=S△ABO+S梯形BOFD+S△DFE,求出即可;
(3)利用勾股定理求出BD,BE,DE,得出△BDE是直角三角形,再利用
| AO |
| BD |
| BO |
| BE |
| ||
| 2 |
解答:解:( 1)由已知得:
,
解得:c=3,b=2,
∴抛物线的线的解析式为y=-x2+2x+3;
(2)由顶点坐标公式得顶点坐标为(1,4)
所以对称轴为x=1,A,E关于x=1对称,
所以E(3,0),
设对称轴与x轴的交点为F,
所以四边形ABDE的面积=S△ABO+S梯形BOFD+S△DFE,
=
AO•BO+
(BO+DF)•OF+
EF•DF
=
×1×3+
(3+4)×1+
×2×4=9;
(3)相似.
如图,作BG⊥DF,
BD=
=
=
,
BE=
=
=3
,
DE=
=
=2
,
所以BD2+BE2=20,DE2=20,
即:BD2+BE2=DE2,所以△BDE是直角三角形,
所以∠AOB=∠DBE=90°,且
=
=
,
所以△AOB∽△DBE.
|
解得:c=3,b=2,
∴抛物线的线的解析式为y=-x2+2x+3;
(2)由顶点坐标公式得顶点坐标为(1,4)
所以对称轴为x=1,A,E关于x=1对称,
所以E(3,0),
设对称轴与x轴的交点为F,
所以四边形ABDE的面积=S△ABO+S梯形BOFD+S△DFE,
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |

(3)相似.
如图,作BG⊥DF,
BD=
| BG2+DG2 |
| 12+12 |
| 2 |
BE=
| BO2+OE2 |
| 32+32 |
| 2 |
DE=
| DF2+EF2 |
| 22+42 |
| 5 |
所以BD2+BE2=20,DE2=20,
即:BD2+BE2=DE2,所以△BDE是直角三角形,
所以∠AOB=∠DBE=90°,且
| AO |
| BD |
| BO |
| BE |
| ||
| 2 |
所以△AOB∽△DBE.
点评:此题主要考查了待定系数法求二次函数解析式以及四边形面积求法和勾股定理、相似三角形的判定等知识,根据已知结合坐标系得出BD,BE,DE的长,利用数形结合得出是解决问题的关键.

练习册系列答案
相关题目
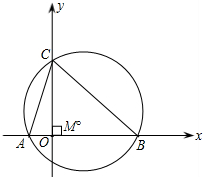 与y轴交点C的纵坐标为3,△ABC的外接圆的圆心为点M.
与y轴交点C的纵坐标为3,△ABC的外接圆的圆心为点M. 此抛物线上,矩形面积为12,
此抛物线上,矩形面积为12, (2013•宁化县质检)已知:如图,抛物线y=ax2+bx+c与x轴交于点A(
(2013•宁化县质检)已知:如图,抛物线y=ax2+bx+c与x轴交于点A( 已知,如图,抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A,B,点A的坐标为(4,0).
已知,如图,抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A,B,点A的坐标为(4,0). 已知,如图,抛物线y=x2+px+q与x轴相交于A、B两点,与y轴交于点C,且OA≠OB,OA=OC,设抛物线的顶点为点P,直线PC与x轴的交点D恰好与点A关于y轴对称.
已知,如图,抛物线y=x2+px+q与x轴相交于A、B两点,与y轴交于点C,且OA≠OB,OA=OC,设抛物线的顶点为点P,直线PC与x轴的交点D恰好与点A关于y轴对称.