Question

已知△ABC的三个旁心为O₁，O₂，O₃．求证：△O₁O₂O₃是锐角三角形．

Answer 1

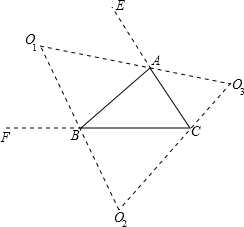证明：∠EAB+∠FBA=（∠ABC+∠BCA）+（∠BAC+∠BCA），
=180°+∠ACB，
∴（∠EAB+∠FBA）=90°+∠ACB，
∴∠O₁=180°-（∠EAB+∠FBA），
=90°-∠ACB，
∴∠O₁是锐角，
同理∠O₂，∠O₃也是锐角，
∴△O₁O₂O₃是锐角三角形．
分析：根据三角形的外角性质，求出∠EAB+∠FBA=180°+∠ACB，求出∠EAB+∠FBA的一半，根据三角形的内角和定理求出∠O₁
=90°-∠ACB，即是锐角，同理∠O₂，∠O₃也是锐角，即可得到答案．
点评：本题主要考查对三角形的五心，三角形的内角和定理，三角形的外角性质，三角形的角平分线等知识点的理解和掌握，题型较好，有一定的难度．