Question

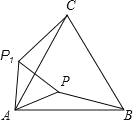
【题目】△ABC 是等边三角形，点 P 在△ABC 内，PA=2，将△PAB 绕点 A 逆时针旋转得到△P1AC，则 P1P 的长等于（ ）

A. 2 B. C. D. 1

Answer 1

【答案】A

【解析】

根据等边三角形的性质推出 AC=AB，∠CAB=60°，根据旋转的性质得出

△CP1A≌△BPA，推出AP1=AP，∠CAP1=∠BAP，求出∠PAP1=60°，得出△APP1

是等边三角形，即可求出答案．

解：∵△ABC 是等边三角形，

∴AC=AB，∠CAB=60°，

∵将△PAB 绕点 A 逆时针旋转得到△P1AC，

∴△CP1A≌△BPA，

∴AP1=AP，∠CAP1=∠BAP，

∴∠CAB=∠CAP+∠BAP=∠CAP+∠CAP1=60°， 即∠PAP1=60°，

∴△APP1 是等边三角形，

∴P1P=PA=2，

故选：A．