题目内容
如图,已知抛物线 与x轴相交于A、B两点,其对称轴为直线x=2,且与x轴交于点D,AO=1.
与x轴相交于A、B两点,其对称轴为直线x=2,且与x轴交于点D,AO=1.(1)填空:b=______,c=______,点B的坐标为(______,______):
(2)若线段BC的垂直平分线EF交BC于点E,交x轴于点F.求FC的长;
(3)探究:在抛物线的对称轴上是否存在点P,使⊙P与x轴、直线BC都相切?若存在,请求出点P的坐标;若不存在,请说明理由.

【答案】分析:(1)根据对称轴和OA=1求出A、B的坐标,代入解析式求出b、c即可;
(2)求出C(2,4)求得E的坐标为(3.5,2)和直线BC的表达式为 ,设直线EF的表达式为y=kx+b,根据EF为BC的中垂线求出
,设直线EF的表达式为y=kx+b,根据EF为BC的中垂线求出 和
和 推出直线EF的表达式为
推出直线EF的表达式为 ,令y=0,得
,令y=0,得 即可求出答案;
即可求出答案;
(3)作∠OBC的平分线交DC于点P,设P(2,a),根据抛物线解析式求出顶点C的坐标与点B的坐标,然后利用∠BCD的正弦列式即可求解.
解答: 解:(1)∵抛物线
解:(1)∵抛物线 与x轴相交于A、B两点,其对称轴为直线x=2,且与x轴交于点D,AO=1,
与x轴相交于A、B两点,其对称轴为直线x=2,且与x轴交于点D,AO=1,
∴A(-1,0),B(5,0),
代入解析式得: ,
,
解得:b= ,c=
,c= ,
,
故答案为: ,
, ,5,0.
,5,0.
(2)由(1)求得 ,
,
∴C(2,4)
∵E为BC的中点,由中点坐标公式求得E的坐标为(3.5,2),
直线BC的表达式为y=- x+
x+ ,
,
整理得4x+3y-20=0
设直线EF的表达式为y=kx+b(k≠0),
∵EF为BC的中垂线,
∴EF⊥BC,
∵互相垂直的两条直线的斜率的积是-1,
∴ ,
,
把E(3.5,2)代入求得 ,
,
∴直线EF的表达式为 ,
,
在 中,令y=0,得
中,令y=0,得 ,
,
∴F( ,0),
,0),
∴FC=FB= ,
,
答:FC的长是 .
.
(3)存在.
作∠OBC的平分线交DC于点P,则P满足条件,
设P(2,a),则P到x轴的距离为等于P到直线BC的距离,都是|a|,
∵抛物线解析式是y=- (x-2)2+4,
(x-2)2+4,
∴点C的坐标是(2,4),
又∵点B的坐标是(5,0),
∴CD=4,DB=5-2=3,
∴BC= =
= =5,
=5,
∵⊙P与x轴、直线BC都相切,
∴∠CEP=∠CDB=90°,
∴∠PCE+∠CPE=90°,∠CBA+∠CPE=90°,
∴∠CPE=∠CBA,
∴sin∠BCD= =
= ,
,
解得:a= ,
,
当P在x轴的下方时,同法得出 =
= ,
,
解得:a=-6,
∴点P的坐标是P(2,-6)或P(2, ).
).
答:在抛物线的对称轴上存在点P,使⊙P与x轴、直线BC都相切,点P的坐标是(2,-6),(2, ).
).
点评:本题主要考查对解二元一次方程组,二次函数图象上点的坐标特征,用待定系数法求二次函数的解析式,勾股定理,线段的垂直平分线定理等知识点的理解和掌握,熟练地运用这些性质进行计算是解此题的关键.
(2)求出C(2,4)求得E的坐标为(3.5,2)和直线BC的表达式为
 ,设直线EF的表达式为y=kx+b,根据EF为BC的中垂线求出
,设直线EF的表达式为y=kx+b,根据EF为BC的中垂线求出 和
和 推出直线EF的表达式为
推出直线EF的表达式为 ,令y=0,得
,令y=0,得 即可求出答案;
即可求出答案;(3)作∠OBC的平分线交DC于点P,设P(2,a),根据抛物线解析式求出顶点C的坐标与点B的坐标,然后利用∠BCD的正弦列式即可求解.
解答:
 解:(1)∵抛物线
解:(1)∵抛物线 与x轴相交于A、B两点,其对称轴为直线x=2,且与x轴交于点D,AO=1,
与x轴相交于A、B两点,其对称轴为直线x=2,且与x轴交于点D,AO=1,∴A(-1,0),B(5,0),
代入解析式得:
 ,
,解得:b=
 ,c=
,c= ,
,故答案为:
 ,
, ,5,0.
,5,0.(2)由(1)求得
 ,
,∴C(2,4)
∵E为BC的中点,由中点坐标公式求得E的坐标为(3.5,2),
直线BC的表达式为y=-
 x+
x+ ,
,整理得4x+3y-20=0
设直线EF的表达式为y=kx+b(k≠0),
∵EF为BC的中垂线,
∴EF⊥BC,
∵互相垂直的两条直线的斜率的积是-1,
∴
 ,
,把E(3.5,2)代入求得
 ,
,∴直线EF的表达式为
 ,
,在
 中,令y=0,得
中,令y=0,得 ,
,∴F(
 ,0),
,0),∴FC=FB=
 ,
,答:FC的长是
 .
.(3)存在.
作∠OBC的平分线交DC于点P,则P满足条件,
设P(2,a),则P到x轴的距离为等于P到直线BC的距离,都是|a|,
∵抛物线解析式是y=-
 (x-2)2+4,
(x-2)2+4,∴点C的坐标是(2,4),
又∵点B的坐标是(5,0),
∴CD=4,DB=5-2=3,
∴BC=
 =
= =5,
=5,∵⊙P与x轴、直线BC都相切,
∴∠CEP=∠CDB=90°,
∴∠PCE+∠CPE=90°,∠CBA+∠CPE=90°,
∴∠CPE=∠CBA,
∴sin∠BCD=
 =
= ,
,解得:a=
 ,
,当P在x轴的下方时,同法得出
 =
= ,
,解得:a=-6,
∴点P的坐标是P(2,-6)或P(2,
 ).
).答:在抛物线的对称轴上存在点P,使⊙P与x轴、直线BC都相切,点P的坐标是(2,-6),(2,
 ).
).点评:本题主要考查对解二元一次方程组,二次函数图象上点的坐标特征,用待定系数法求二次函数的解析式,勾股定理,线段的垂直平分线定理等知识点的理解和掌握,熟练地运用这些性质进行计算是解此题的关键.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
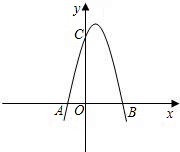 如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).
如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).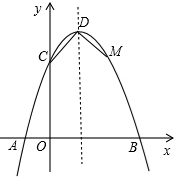 如图,已知抛物线与x轴交于点A(-1,0),与y轴交于点C(0,3),且对称轴方程为x=1
如图,已知抛物线与x轴交于点A(-1,0),与y轴交于点C(0,3),且对称轴方程为x=1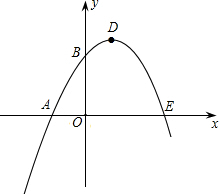 函数的最大值是4.
函数的最大值是4. (2012•株洲)如图,已知抛物线与x轴的一个交点A(1,0),对称轴是x=-1,则该抛物线与x轴的另一交点坐标是( )
(2012•株洲)如图,已知抛物线与x轴的一个交点A(1,0),对称轴是x=-1,则该抛物线与x轴的另一交点坐标是( )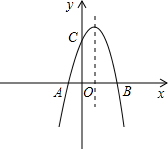 如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).
如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).