��Ŀ����
���˰��涨�ļ�������ij��ҩ���÷�ҩ��2Сʱ��ÿ����ѪҺ�еĺ�ҩ���ﵽ���ֵΪ4���ˣ���֪��ҩ��2Сʱǰÿ����ѪҺ�еĺ�ҩ��y�����ˣ���ʱ��x��Сʱ������������2Сʱ��y��x�ɷ���������ͼ��ʾ��������������Ϣ����������⣺
��С��1����0��x��2ʱ��y��x�ĺ�����ϵʽ
��С��2����x>2ʱ��y��x�ĺ�����ϵʽ
��С��3����ÿ����ѪҺ�еĺ�ҩ��������2����ʱ������Ч�����ҩһ�Σ����Ƽ�������Чʱ���Ƕ��
��С��1����0��x��2ʱ����y=kx
�ѣ�2��4������ã�k=2��
��y=2x��
��С��2����x��2ʱ����y= ��
��
�ѣ�2��4������ã�m=8��
��y=
��С��3����y=2ʱ����
X1=1��x2=4��
����Чʱ��=4-1=3Сʱ��
�����Ƽ�������Чʱ����3Сʱ
����

��ϰ��ϵ�д�
 ˫��ͬ������ѵ��ϵ�д�
˫��ͬ������ѵ��ϵ�д� �Ƹ�С״Ԫͬ������������ϵ�д�
�Ƹ�С״Ԫͬ������������ϵ�д�
�����Ŀ
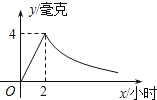 ���˰��涨�ļ�������ij��ҩ���÷�ҩ��2Сʱ��ÿ����ѪҺ�еĺ�ҩ���ﵽ���ֵΪ4���ˣ���֪��ҩ��2Сʱǰÿ����ѪҺ�еĺ�ҩ��y�����ˣ���ʱ��x��Сʱ������������2Сʱ��y��x�ɷ���������ͼ��ʾ��������������Ϣ����������⣮
���˰��涨�ļ�������ij��ҩ���÷�ҩ��2Сʱ��ÿ����ѪҺ�еĺ�ҩ���ﵽ���ֵΪ4���ˣ���֪��ҩ��2Сʱǰÿ����ѪҺ�еĺ�ҩ��y�����ˣ���ʱ��x��Сʱ������������2Сʱ��y��x�ɷ���������ͼ��ʾ��������������Ϣ����������⣮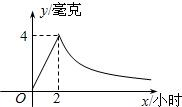 ��ͼ�����˰��涨�ļ�������ijҩ���÷�ҩ��2Сʱ��ÿ����ѪҺ�к�ҩ���ﵽ���ֵΪ4���ˣ���֪��ҩ��2Сʱǰÿ����ѪҺ�к�ҩ��y�����ˣ���ʱ��x��Сʱ������������2Сʱ��y��x�ɷ�������
��ͼ�����˰��涨�ļ�������ijҩ���÷�ҩ��2Сʱ��ÿ����ѪҺ�к�ҩ���ﵽ���ֵΪ4���ˣ���֪��ҩ��2Сʱǰÿ����ѪҺ�к�ҩ��y�����ˣ���ʱ��x��Сʱ������������2Сʱ��y��x�ɷ�������

