题目内容
(1)计算:-22+(tan60°-1)× +(-
+(- )-2+(-π)0-|2-
)-2+(-π)0-|2- |
|
(2)先化简,再求值: ,其中x=
,其中x=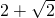 .
.
(3)解方程组: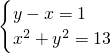 .
.
解:(1)-22+(tan60°-1)× +(-
+(- )-2+(-π)0-|2-
)-2+(-π)0-|2- |
|
=-4+( 1)×
1)× +4+1-2+
+4+1-2+
=-4+3- +4+1-2
+4+1-2
=2;
(2)
=[ -
- ]×
]×
=[ -
- ]×
]×
= ×
×
= ,
,
把x=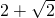 代入上式得:
代入上式得:
原式= =
= ;
;
(3)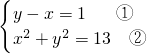 ,
,
由①得:y=1+x③,
把③代入②得x2+(1+x)2=13,
解得:x1=2,x2=-3;
把x1=2代入③得:y1=3,
把x2=-3代入③得:y2=-2,
则原方程组的解是: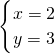 或
或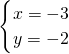 .
.
分析:(1)根据零指数幂、负整数指数幂、三角函数的概念和绝对值的性质分别进行计算,再把所得的结果合并即可;
(2)先根据分式的减法和除法运算法则把分式化简,再代入x的值即可;
(3)先由①求出y=1+x,再代入②求出x的值,再把x的值分别代入③即可得出答案.
点评:此题考查了高次方程,用到的知识点是分式的化简求值、零指数幂、负整数指数幂、三角函数和解方程组,解题的关键是综合应用有关运算法则.
 +(-
+(- )-2+(-π)0-|2-
)-2+(-π)0-|2- |
|=-4+(
 1)×
1)× +4+1-2+
+4+1-2+
=-4+3-
 +4+1-2
+4+1-2
=2;
(2)

=[
 -
- ]×
]×
=[
 -
- ]×
]×
=
 ×
×
=
 ,
,把x=
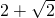 代入上式得:
代入上式得:原式=
 =
= ;
;(3)
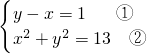 ,
,由①得:y=1+x③,
把③代入②得x2+(1+x)2=13,
解得:x1=2,x2=-3;
把x1=2代入③得:y1=3,
把x2=-3代入③得:y2=-2,
则原方程组的解是:
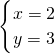 或
或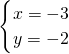 .
.分析:(1)根据零指数幂、负整数指数幂、三角函数的概念和绝对值的性质分别进行计算,再把所得的结果合并即可;
(2)先根据分式的减法和除法运算法则把分式化简,再代入x的值即可;
(3)先由①求出y=1+x,再代入②求出x的值,再把x的值分别代入③即可得出答案.
点评:此题考查了高次方程,用到的知识点是分式的化简求值、零指数幂、负整数指数幂、三角函数和解方程组,解题的关键是综合应用有关运算法则.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目