题目内容
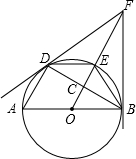
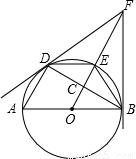
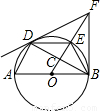
由⊙O外一点F作⊙O的两条切线，切点分别为B、D，AB是⊙O的直径，连接AD、BD，线段OF交⊙O于E，交
BD于C，连接DE、BE．有下列序号为①～④的四个结论：
①BE=DE；②∠EBD=∠EDB；③DE∥AB；④BD2=2AD•FC
其中正确的结论有________．（把你认为正确结论的序号全部填上）
①②④
分析：根据已知对各个结论进行分析，从而确定正确答案．
解答：∵BF，DF是⊙O的两条切线
∴OF是∠DFB的角平分线，DF=FB，FO⊥BD，CD=CB
∴
=
∴BE=DE（①正确）
∵=
∴∠EBD=∠EDB（②正确）
∵FB切⊙O于B
∴FB⊥OB
∵BC⊥OF
∵BC2=OC•FC
∴（
BD）2=OC•CE
∵OC为△ABD的中位线
∴OC=AD
∴（BD）2=AD•CE
∴BD2=2AD•FC（④正确）
故其中正确的结论有①②④．
点评：此题比较复杂，涉及到角平分线的性质，切线长定理，圆周角定理及三角形的中位线定理等知识点的综合运用．
分析：根据已知对各个结论进行分析，从而确定正确答案．
解答：∵BF，DF是⊙O的两条切线
∴OF是∠DFB的角平分线，DF=FB，FO⊥BD，CD=CB
∴
=∴BE=DE（①正确）
∵
=∴∠EBD=∠EDB（②正确）
∵FB切⊙O于B
∴FB⊥OB
∵BC⊥OF
∵BC2=OC•FC
∴（
BD）2=OC•CE∵OC为△ABD的中位线
∴OC=
AD∴（
BD）2=AD•CE∴BD2=2AD•FC（④正确）
故其中正确的结论有①②④．
点评：此题比较复杂，涉及到角平分线的性质，切线长定理，圆周角定理及三角形的中位线定理等知识点的综合运用．
练习册系列答案
全能练考卷系列答案
相关题目
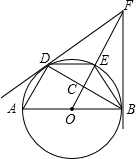
BD于C，连接DE、BE．有下列序号为①～④的四个结论：
