题目内容
探究:在图甲中,已知点E、F分别为线段AB、CD的中点.
①若A(-1,0),B(3,0),则E点的坐标为________;
②若C(-2,+2),D(-2,-1),点则F点坐标为________.
归纳:无论线段AB处于直角坐标系中的哪个位置,当其端点为A(a,b),B(c,d),AB中点坐标为(x,y)时,x=________,y=________.(用含a,b,c,d的代数式表示,不必证明)
运用:在图乙中,一次函数与反比例函数的图象交点为A(-1,-3),B(3,1).
①此一次函数和反比例函数的解析式分别为________;
②若以A,O,B,P为顶点的四边形是平行四边形,请利用上面的结论求出顶点P的坐标.
(1,0) (-2, )
) 
 y=x-2,y=
y=x-2,y=
分析:探究:①利用图形可确定E点坐标为(1,0);②利用图形可确定线段CD的中点F的坐标;
运用利用线段中点坐标公式求解;
归纳:①运用待定系数法求两函数的解析式;
②分类讨论:当以AB为对角线时,四边形OAPB为平行四边形,对角线交与点Q,根据平行四边形的性质得到Q为AB的中点,Q点为PO的中点,先利用归纳中的结论由A、B坐标确定Q点坐标,然后由点O与Q点坐标确定P点坐标;同理可确定当OB和OA为对角线时对应的P点坐标.
解答:探究:①点E的横坐标为 =1,纵坐标为
=1,纵坐标为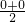 ,则E点坐标为(1,0);
,则E点坐标为(1,0);
②F点的横坐标为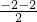 =-2,纵坐标为
=-2,纵坐标为 =
= ,则F点的坐标为(-2,
,则F点的坐标为(-2, );
);
归纳:x= ,y=
,y= ;
;
运用:①设直线AB的解析式为y=kx+b,把A(-1,-3),B(3,1)代入得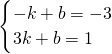 ,解得
,解得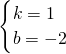 ,
,
所以直线AB的解析式为y=x-2;
设反比例函数解析式为y=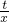 ,
,
把A(-1,-3)代入得t=-1×(-3)=3,
所以反比例函数解析式为y= ;
;
②当以AB为对角线时,四边形OAPB为平行四边形,对角线交与点Q,
∴Q为AB的中点,Q点为PO的中点,
∴Q点坐标为( ,
,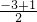 ),即Q(1,-1),
),即Q(1,-1),
设P点坐标为(m,n),则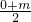 =1,
=1,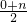 =-1,解得m=2,n=-2,
=-1,解得m=2,n=-2,
∴P点坐标为(2,-2);
同理可得当以OB为对角线时,四边形OABP为平行四边形,此时P点坐标为(4,4);当以OA为对角线时,四边形OPAB为平行四边形,此时P点坐标为(-4,-4),
∴满足条件的P点坐标为(2,-2)或(4,4)或(-4,-4).
故答案为(1,0);(-2, );
); ,
, ;y=x-2,y=
;y=x-2,y= .
.
点评:本题考查了反比例函数的综合题:掌握反比例函数图象上点的坐标特征和待定系数法求函数解析式、平时四边形的判定与性质.
 )
) 
 y=x-2,y=
y=x-2,y=
分析:探究:①利用图形可确定E点坐标为(1,0);②利用图形可确定线段CD的中点F的坐标;
运用利用线段中点坐标公式求解;
归纳:①运用待定系数法求两函数的解析式;
②分类讨论:当以AB为对角线时,四边形OAPB为平行四边形,对角线交与点Q,根据平行四边形的性质得到Q为AB的中点,Q点为PO的中点,先利用归纳中的结论由A、B坐标确定Q点坐标,然后由点O与Q点坐标确定P点坐标;同理可确定当OB和OA为对角线时对应的P点坐标.
解答:探究:①点E的横坐标为
 =1,纵坐标为
=1,纵坐标为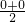 ,则E点坐标为(1,0);
,则E点坐标为(1,0);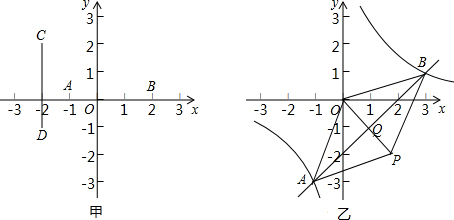
②F点的横坐标为
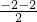 =-2,纵坐标为
=-2,纵坐标为 =
= ,则F点的坐标为(-2,
,则F点的坐标为(-2, );
);归纳:x=
 ,y=
,y= ;
;运用:①设直线AB的解析式为y=kx+b,把A(-1,-3),B(3,1)代入得
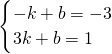 ,解得
,解得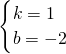 ,
,所以直线AB的解析式为y=x-2;
设反比例函数解析式为y=
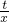 ,
,把A(-1,-3)代入得t=-1×(-3)=3,
所以反比例函数解析式为y=
 ;
;②当以AB为对角线时,四边形OAPB为平行四边形,对角线交与点Q,
∴Q为AB的中点,Q点为PO的中点,
∴Q点坐标为(
 ,
,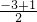 ),即Q(1,-1),
),即Q(1,-1),设P点坐标为(m,n),则
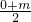 =1,
=1,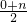 =-1,解得m=2,n=-2,
=-1,解得m=2,n=-2,∴P点坐标为(2,-2);
同理可得当以OB为对角线时,四边形OABP为平行四边形,此时P点坐标为(4,4);当以OA为对角线时,四边形OPAB为平行四边形,此时P点坐标为(-4,-4),
∴满足条件的P点坐标为(2,-2)或(4,4)或(-4,-4).
故答案为(1,0);(-2,
 );
); ,
, ;y=x-2,y=
;y=x-2,y= .
.点评:本题考查了反比例函数的综合题:掌握反比例函数图象上点的坐标特征和待定系数法求函数解析式、平时四边形的判定与性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 定义:若某个图形可分割为若干个都与他相似的图形,则称这个图形是自相似图形.
定义:若某个图形可分割为若干个都与他相似的图形,则称这个图形是自相似图形.