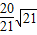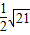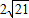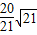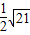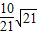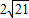题目内容
（2000•兰州）有两个同心圆，大圆的直径AB交小圆于C、D，大圆的弦EF切小圆于C点，ED交小圆于G点，若AO=6，CO=4，则EG等于（ ）A．
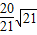
B．
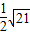
C．
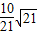
D．
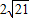
【答案】分析：连接OE，在Rt△OCE中，由勾股定理可求出CE的长；同理可在Rt△ECD中，由勾股定理求得ED的长；由于EC是小圆的切线，ED是小圆的割线，根据切割线定理即可求得EG的长．
解答：
解：如图，连接OE；
∵EF是小圆的切线，
∴OC⊥EF；
Rt△ECO中，OE=OA=6，OC=4，
由勾股定理，得：EC=
=2
；
Rt△ECD中，CD=8，
由勾股定理，得：ED=
=2
；
已知EF切小圆于C，由切割线定理，得：
EG=EC2÷ED=（2
）2÷2
=
．
故选C．
点评：此题主要考查了切线的性质、勾股定理及圆切割线定理的应用．
解答：
解：如图，连接OE；∵EF是小圆的切线，
∴OC⊥EF；
Rt△ECO中，OE=OA=6，OC=4，
由勾股定理，得：EC=
=2；Rt△ECD中，CD=8，
由勾股定理，得：ED=
=2；已知EF切小圆于C，由切割线定理，得：
EG=EC2÷ED=（2
）2÷2=．故选C．
点评：此题主要考查了切线的性质、勾股定理及圆切割线定理的应用．
练习册系列答案
学业测评一课一测系列答案
相关题目
