题目内容
已知抛物线![]() .
.
1.试说明:无论m为何实数,该抛物线与x轴总有两个不同的交点;
2.如图,当抛物线的对称轴为直线x=3时,抛物线的顶点为点C,直线y=x﹣1与抛物线交于A、B两点,并与它的对称轴交于点D.
①抛物线上是否存在一点P使得四边形ACPD是正方形?若存在,求出点P的坐标;若不存在,说明理由;
②平移直线CD,交直线AB于点M,交抛物线于点N,通过怎样的平移能使得以C、D、M、N为顶点的四边形是平行四边形?(直接写出平移的方法,不要说明理由)
1.该抛物线与x轴总有两个不同的交点
2.点P坐标为(5,0);平行四边形
解析:解:⑴ 该函数的判别式=m2﹣4m+7=(m﹣2)2+3>0
∴该抛物线与x轴总有两个不同的交点;……………………………………3分

⑵ 由直线y=x﹣1与抛物线交于A、B两点,∴点A(1,0)代入二次函数式则m=3
∴二次函数式为:![]() ……………………………………4分
……………………………………4分
当抛物线的对称轴为直线x=3时,则y=﹣2,
即顶点C为(3,﹣2),……………………………………5分
把x=3代入直线y=x﹣1则y=2,
即点D(3,2) ……………………………………6分
设点P(x,![]() ),如右图所示:
),如右图所示:
由题意知: PH=CH,(或PH=DH)
则![]()
解得:x=3或x=5 ……………………………………8分
则点P(3,2)(与点D重合舍去)或(5,0)
经检验点(5,0)符合,
所以点P坐标为(5,0);……………………………………9分
(注:其它方法酌情给分)
②把直线CD向右平移1+![]() 个单位或2个单位,向左平移
个单位或2个单位,向左平移![]() ﹣1个单位,能使得以C、D、M、N为顶点的四边形是平行四边形.
﹣1个单位,能使得以C、D、M、N为顶点的四边形是平行四边形.

练习册系列答案
相关题目
 (2013•吉安模拟)如图,在平面直角坐标系中,直线AD与抛物线y=-x2+bx+c交于A(-1,0)和D(2,3)两点,点C、F分别为该抛物线与y轴的交点和顶点.
(2013•吉安模拟)如图,在平面直角坐标系中,直线AD与抛物线y=-x2+bx+c交于A(-1,0)和D(2,3)两点,点C、F分别为该抛物线与y轴的交点和顶点.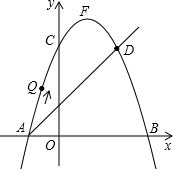 如图,在平面直角坐标系中,直线AD与抛物线y=-x2+bx+c交于A(-1,0)和D(2,3)两点,点C、F分别为该抛物线与y轴的交点和顶点.
如图,在平面直角坐标系中,直线AD与抛物线y=-x2+bx+c交于A(-1,0)和D(2,3)两点,点C、F分别为该抛物线与y轴的交点和顶点.
