题目内容
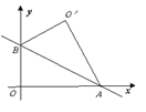
【题目】如图,抛物线y=![]() +bx+c与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
+bx+c与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,△CBF的面积最大?求出△CBF的最大面积及此时E点的坐标.

【答案】(1)y=![]() +
+![]() x+2;(2)存在.P(
x+2;(2)存在.P(![]() ,4)或(
,4)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() );(3) 当E运动到BC的中点时,△EBC面积最大,△EBC最大面积是4,此时E(2,1).
);(3) 当E运动到BC的中点时,△EBC面积最大,△EBC最大面积是4,此时E(2,1).
【解析】
试题分析:(1)把A(﹣1,0),C(0,2)代入y=![]() +bx+c列方程组即可;
+bx+c列方程组即可;
(2)先求出CD的长,分两种情形①当CP=CD时,②当DC=DP时分别求解即可;
(3)求出直线BC的解析式,设E(m,![]() ),则F(m,
),则F(m,![]() ),构建二次函数,利用二次函数的性质即可解决问题.
),构建二次函数,利用二次函数的性质即可解决问题.
试题解析:(1)把A(﹣1,0),C(0,2)代入y=![]() +bx+c得
+bx+c得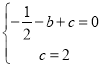 ,
,
解得b=![]() ,c=2,
,c=2,
∴抛物线的解析式为y=![]() +
+![]() x+2;
x+2;
(2)存在.如图1中,∵C(0,2),D(![]() ,0),
,0),
∴OC=2,OD=![]() ,CD=
,CD=![]() =
=![]() ,
,

①当CP=CD时,可得![]() (
(![]() ,4),
,4),
②当DC=DP时,可得![]() (
(![]() ,
,![]() ),
),![]() (
(![]() ,
,![]() ),
),
综上所述,满足条件的P点的坐标为(![]() ,4)或(
,4)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() );
);
(3)如图2中,
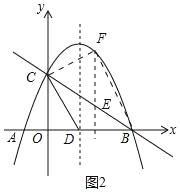
对于抛物线y=![]() +
+![]() x+2,当y=0时,
x+2,当y=0时,![]() +
+![]() x+2=0,解得
x+2=0,解得![]() =4,
=4,![]() =﹣1,
=﹣1,
∴B(4,0),A(﹣1,0),
由B(4,0),C(0,2)得直线BC的解析式为y=![]() x+2,
x+2,
设E(m,![]() ),则F(m,
),则F(m,![]() ),
),
EF=(![]() )﹣(
)﹣(![]() )=
)=![]() =
=![]() ,
,
∴![]() <0,∴当m=2时,EF有最大值2,
<0,∴当m=2时,EF有最大值2,
此时E是BC中点,
∴当E运动到BC的中点时,△EBC面积最大,
∴△EBC最大面积=![]() ×4×EF=
×4×EF=![]() ×4×2=4,此时E(2,1).
×4×2=4,此时E(2,1).

 阅读快车系列答案
阅读快车系列答案