Question

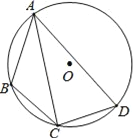
【题目】如图，已知AB是⊙O的直径，AB＝4，点C是AB延长线上一点，且BC＝2，点D是半圆的中点，点P是⊙O上任意一点．

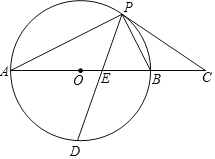
（1）当PD与AB交于点E且PC＝CE时，求证：PC与⊙O相切；

（2）在（1）的条件下，求PC的长；

（3）点P是⊙O上动点，当PD+PC的值最小时，求PC的长．

Answer 1

【答案】（1）详见解析；（2）2；（3）

【解析】

（1）根据点D是半圆的中点可得，∠APD＝45°，根据圆的半径相等和三角形的外角性质可推出∠PEC＝90°﹣∠OPE，根据PC＝CE即可证得；

（2）在△OPC中，由勾股定理即可求出PC的长；

（3）根据两点之间线段最短可知，当点C、P、D三点共线时，PD+PC最小，根据圆内接四边形的性质和已知条件可证得△CBP'∽△CDA，利用对应边成比例即可求出答案．

（1）证明：如图1，

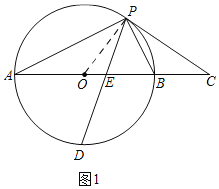
∵点D是半圆的中点，

∴∠APD＝45°，

连接OP，

∴OA＝OP，

∴∠OAP＝∠OPA，

∴∠PEC＝∠OAP+∠APE＝∠OPA+∠APE＝∠APE﹣∠OPE+∠APE＝2∠APE﹣∠OPE＝90°﹣∠OPE，

∵PC＝EC，

∴∠CPE＝∠PEC＝90°﹣∠APE，

∴∠OPC＝∠OPE+∠CPE＝∠OPE+90°﹣∠OPE＝90°，

∵点P在⊙O上，

∴PC是⊙O的切线；

（2）解：由（1）知，∠OPC＝90°，

∵AB＝4，

∴OP＝OB＝AB＝2，

∵BC＝2，

∴OC＝OB+BC＝4，

根据勾股定理得，；

（3）解：连接OD，如图2，

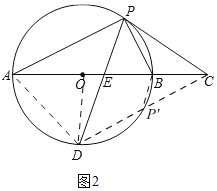
∵D是半圆O的中点，

∴∠BOD＝90°，要使PD+PC的值最小，则连接CD交⊙O于P'，

即点P在P'的位置时，PD+PC最小，

由（2）知，OC＝4，

在Rt△COD中，OD＝OB＝2，

根据勾股定理得，，

连接BP，AD，则四边形ADP'B是⊙O的内接四边形，

∴∠CBP'＝∠CDA，

∵∠BCP＝∠DCA，

∴△CBP'∽△CDA，

∴，

∴，

∴CP'＝，

∴当PD+PC的值最小时，PC=．