题目内容
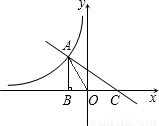
如图,直线AC与双曲线y=| k |
| x |
| 13 |
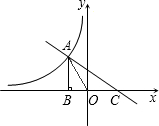
 点A的横坐标为2,过点A作AB⊥x轴于点B,且S△ABC:S△ABO=4:1.
点A的横坐标为2,过点A作AB⊥x轴于点B,且S△ABC:S△ABO=4:1.(1)求k的值及直线AC的解析式;
(2)在第四象限内,双曲线y=
| k |
| x |
分析:(1)由AO=
,点A的横坐标为2,易求AB=3,则A(2,-3),可求反比例函数解析式;由S△ABC:S△ABO=4:1,可得BC=8,OC=6,则C(-6,0),由A、C坐标可求直线AC的解析式;
(2)BC长度已知,用m的式子表示高(D点纵坐标)即可表示面积S.
| 13 |
(2)BC长度已知,用m的式子表示高(D点纵坐标)即可表示面积S.
解答:解:(1)∵OA=
,OB=2,在直角三角形OAB中,根据勾股定理有:AB=3.
∴A(2,-3).由于反比例函数过A点,
∴k=xy=-6.
∵S△ABC:S△ABO=4:1,
∴BC=4OB=8,OC=6
∴C(-6,0).
设直线AC的解析式为y=kx+b,则有:
,
解得
∴直线AC的解析式为y=-
x-
,
(2)根据(1)可知n=
因此S=
BC•|n|=
.
| 13 |
∴A(2,-3).由于反比例函数过A点,
∴k=xy=-6.
∵S△ABC:S△ABO=4:1,
∴BC=4OB=8,OC=6
∴C(-6,0).
设直线AC的解析式为y=kx+b,则有:
|
解得
|
∴直线AC的解析式为y=-
| 3 |
| 8 |
| 9 |
| 4 |
(2)根据(1)可知n=
| -6 |
| m |
因此S=
| 1 |
| 2 |
| 24 |
| m |
点评:本题考查了一次函数及反比例函数解析式的确定、图形的面积求法等知识及综合应用知识、解决问题的能力.

练习册系列答案
相关题目
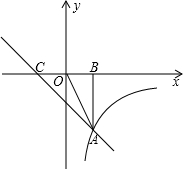
 O|=4,点A的横坐标为-2,过点A作AB⊥x轴于点B,且S△AOC:S△AOB=3:2.
O|=4,点A的横坐标为-2,过点A作AB⊥x轴于点B,且S△AOC:S△AOB=3:2.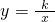 在第二象限交于点A(x0,y0),交x轴的正半轴于点C,且|A
在第二象限交于点A(x0,y0),交x轴的正半轴于点C,且|A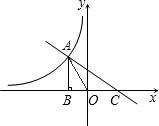 O|=4,点A的横坐标为-2,过点A作AB⊥x轴于点B,且S△AOC:S△AOB=3:2.
O|=4,点A的横坐标为-2,过点A作AB⊥x轴于点B,且S△AOC:S△AOB=3:2.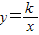 在第二象限交于点A(x,y),交x轴的正半轴于点C,且|AO|=4,点A的横坐标为-2,过点A作AB⊥x轴于点B,且S△AOC:S△AOB=3:2.
在第二象限交于点A(x,y),交x轴的正半轴于点C,且|AO|=4,点A的横坐标为-2,过点A作AB⊥x轴于点B,且S△AOC:S△AOB=3:2.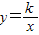 上有一动点P(r,m),设△BCP的面积为S.求S与r的函数关系式.
上有一动点P(r,m),设△BCP的面积为S.求S与r的函数关系式.