Question

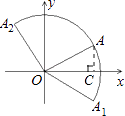
【题目】如图，在平面直角坐标系中，点A（ ，1）关于x轴的对称点为点A1 ， 将OA绕原点O逆时针方向旋转90°到OA2 ， 用扇形OA1A2围成一个圆锥，则该圆锥的底面圆的半径为 ．

Answer 1

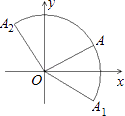
【答案】
【解析】解：过点A作AC⊥x轴于点C，
∵点A的坐标为（ ，1），
∴AO= =2，
∴tan∠AOC= = = ，
∴∠AOC=30°，
∵点A（ ，1）关于x轴的对称点为点A1 ，
∴∠COA1=30°，
∵将OA绕原点O逆时针方向旋转90°到OA2 ，
∴∠A2OA1=∠AOC+∠COA1+∠A2OA=30°+90°+30°=150°，
∴圆锥底面圆的周长为： = = π，
∴该圆锥的底面圆的半径为：2πR= π，
∴R= ．
所以答案是： ．

【考点精析】本题主要考查了圆锥的相关计算的相关知识点，需要掌握圆锥侧面展开图是一个扇形，这个扇形的半径称为圆锥的母线；圆锥侧面积S=πrl；V圆锥=1/3πR2h.才能正确解答此题．