Question

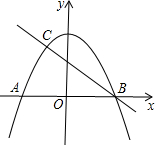如图，抛物线y₁=-

3

4

x²+3与x轴交于A、B两点，与直线y₂=-

3

4

x+b相交于B、C两点．
（1）求直线BC的解析式和点C的坐标；
（2）若对于相同的x，两个函数的函数值满足y₁≥y₂，则自变量x的取值范围是

-1≤x≤2

．

Answer 1

分析：（1）令y=0求解得到点B的坐标，把点B的坐标代入直线解析式求出b的值，再与直线联立求解得到点C的坐标；
（2）根据函数图象找出抛物线在直线上方部分的x的取值范围即可．

解答：解：（1）令y=0，则-

3

4

x²+3=0，
解得x₁=-2，x₂=2，
∴点B的坐标为（2，0），
∴-

3

4

×2+b=0，
解得b=

3

2

，
∴直线BC的解析式为y=-

3

4

x+

3

2

，
由-

3

4

x²+3=-

3

4

x+

3

2

，即3x²-x-6=0，
解得x₁=-1，x₂=2（舍去），
∴点C的坐标为（-1，

9

4

）；

（2）由图可知，y₁≥y₂时，-1≤x≤2．
故答案为：-1≤x≤2．

点评：本题考查了二次函数与不等式，待定系数法求一次函数解析式，抛物线与x轴的交点问题，利用数形结合的思想求解是此类题目解题的关键．