题目内容
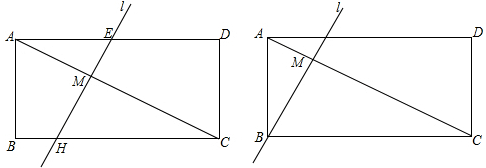
 已知:矩形ABCD中,E为AB的中点,过E点的直线分别交AD和CB的延长线于F、H,AC交FH于G
已知:矩形ABCD中,E为AB的中点,过E点的直线分别交AD和CB的延长线于F、H,AC交FH于G求证:(1)△AEF≌△BEH;
(2)HB•GH=HC•FG.
分析:(1)由E是BC的中点得到AE=BE,由矩形ABCD得到∠FAE=∠EBH=90°,而∠AEF和∠BEH是对顶角,由此即可证明;
(2)由矩形ABCD得到AD∥BC,然后利用平行线的性质得到△AFG∽△CHG,接着利用相似三角形的性质得
=
,根据(1)得到AF=BH,由此即可证明HB•GH=HC•FG.
(2)由矩形ABCD得到AD∥BC,然后利用平行线的性质得到△AFG∽△CHG,接着利用相似三角形的性质得
| AF |
| CH |
| FG |
| HG |
解答:证明:(1)∵E是BC的中点,
∴AE=BE(1分),
∵矩形ABCD,
∴∠FAE=∠EBH=90°,(1分)
∵∠AEF=∠BEH,
∴△AEF≌△BEH(3分);
(2)∵矩形ABCD,
∴AD∥BC,
∴△AFG∽△CHG(1分),
∴
=
(2分),
∵△AEF≌△BEH,
∴AF=BH(1分),
∴HB•GH=HC•FG.(1分)
∴AE=BE(1分),
∵矩形ABCD,
∴∠FAE=∠EBH=90°,(1分)
∵∠AEF=∠BEH,
∴△AEF≌△BEH(3分);
(2)∵矩形ABCD,
∴AD∥BC,
∴△AFG∽△CHG(1分),
∴
| AF |
| CH |
| FG |
| HG |
∵△AEF≌△BEH,
∴AF=BH(1分),
∴HB•GH=HC•FG.(1分)
点评:此题分别考查了全等三角形的性质与判定、相似三角形的性质与判定及矩形的性质,解题时首先利用矩形的性质证明三角形全等,然后利用平行线的性质证明三角形相似,最后利用相似三角形、全等三角形的性质解决问题.

练习册系列答案
相关题目
 ,tan∠DAE=
,tan∠DAE= 已知在矩形ABCD中.
已知在矩形ABCD中. 已知,矩形ABCD中,延长BC至E,使BE=BD,F为DE的中点,连结AF、CF.
已知,矩形ABCD中,延长BC至E,使BE=BD,F为DE的中点,连结AF、CF.