题目内容
解方程：
（1）2x2-x-1=0
（2）（x-2）2=6-3x
（3）（x-2）2=（2x+3）2
（4）2x2-9x+8=0
解：（1）2x2-x-1=0
（2x+1）（x-1）=0，
解得；x1=-
，x2=1；
（2）（x-2）2=6-3x
（x-2）2=3（2-x），
（2-x）2-3（2-x）=0，
（2-x）（2-x-3）=0，
解得：x1=2，x2=-1；
（3）（x-2）2=（2x+3）2
[x-2+（2x+3）][x-2-（2x+3）]=0，
∴（3x+1）（-x-5）=0，
∴x1=-
，x2=-5；
（4）2x2-9x+8=0
b2-4ac=81-4×2×8=17＞0，
x=
，
∴x1=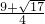
，x2=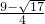
．
分析：（1）直接利用十字相乘法分解因式得出方程的解；
（2）利用提取公因式法分解因式得出方程的解；
（3）利用公式法因式法分解因式得出方程的解；
（4）利用公式法直接求出方程的根．
点评：此题主要考查了因式分解法以及公式法解一元二次方程，正确因式分解是解题关键．
（2x+1）（x-1）=0，
解得；x1=-
，x2=1；（2）（x-2）2=6-3x
（x-2）2=3（2-x），
（2-x）2-3（2-x）=0，
（2-x）（2-x-3）=0，
解得：x1=2，x2=-1；
（3）（x-2）2=（2x+3）2
[x-2+（2x+3）][x-2-（2x+3）]=0，
∴（3x+1）（-x-5）=0，
∴x1=-
，x2=-5；（4）2x2-9x+8=0
b2-4ac=81-4×2×8=17＞0，
x=
，∴x1=
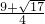，x2=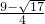．分析：（1）直接利用十字相乘法分解因式得出方程的解；
（2）利用提取公因式法分解因式得出方程的解；
（3）利用公式法因式法分解因式得出方程的解；
（4）利用公式法直接求出方程的根．
点评：此题主要考查了因式分解法以及公式法解一元二次方程，正确因式分解是解题关键．
练习册系列答案
相关题目