题目内容
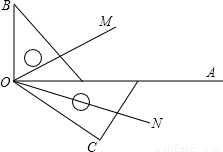
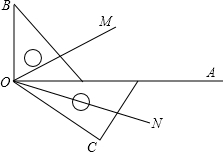 如图,两块三角板摆放在一起,射线OM平分∠BOC、ON平分∠AOC.
如图,两块三角板摆放在一起,射线OM平分∠BOC、ON平分∠AOC.
(1)求∠MON的度数;
(2)如果(1)中,一个三角板绕点O旋转一定角度,使得∠AOC=20°,其它条件不变,求∠MON的度数;
(3)如果(1)中,一个三角板绕点O旋转一定角度,使得∠AOC=α,( α为锐角 ),其它条件不变,求∠MON的度数;
(4)如果(1)中,一个三角板绕点O旋转一定角度,使得∠AOB=β ( β为锐角 ),其它条件不变,求∠MON的度数.
解:(1)∵∠BOC=∠AOB+∠AOC=90°+30°=120°,射线OM平分∠BOC,
∴∠COM= ∠BOC=
∠BOC= ×120°=60°,
×120°=60°,
∵ON平分∠AOC,
∴∠CON= ∠AOC=
∠AOC= ×30°=15°,
×30°=15°,
∴∠MON=∠COM-∠CON=60°-15°=45°;
(2)∵∠BOC=∠AOB+∠AOC=90°+20°=110°,射线OM平分∠BOC,
∴∠COM= ∠BOC=
∠BOC= ×110°=55°,
×110°=55°,
∵ON平分∠AOC,
∴∠CON= ∠AOC=
∠AOC= ×20°=10°,
×20°=10°,
∴∠MON=∠COM-∠CON=55°-10°=45°;
(3)∵∠BOC=∠AOB+∠AOC=90°+α,射线OM平分∠BOC,
∴∠COM= ∠BOC=
∠BOC= ×(90°+α),
×(90°+α),
∵ON平分∠AOC,
∴∠CON= ∠AOC=
∠AOC= α,
α,
∴∠MON=∠COM-∠CON= ×(90°+α)-
×(90°+α)- α=45°+
α=45°+ α-
α- α=45°;
α=45°;
(4))∵∠BOC=∠AOB+∠AOC=β+30°,射线OM平分∠BOC,
∴∠COM= ∠BOC=
∠BOC= (β+30°),
(β+30°),
∵ON平分∠AOC,
∴∠CON= ∠AOC=
∠AOC= ×30°=15°,
×30°=15°,
∴∠MON=∠COM-∠CON= (β+30°)-15°=
(β+30°)-15°= β+15°-15°=
β+15°-15°= β.
β.
分析:(1)根据三角板的度数求出∠BOC的度数,再根据角平分线的定义求出∠COM与∠CON的度数,然后根据∠MON=∠COM-∠CON,代入数据进行计算即可得解;
(2)先求出∠BOC的度数,再根据角平分线的定义求出∠COM与∠CON的度数,然后根据∠MON=∠COM-∠CON,代入数据进行计算即可得解;
(3)∠BOC的度数,再根据角平分线的定义求出∠COM与∠CON的度数,然后根据∠MON=∠COM-∠CON,代入数据进行计算即可得解;
(4)∠BOC的度数,再根据角平分线的定义求出∠COM与∠CON的度数,然后根据∠MON=∠COM-∠CON,代入数据进行计算即可得解;
点评:本题考查了角的计算以及旋转的性质,认准图形,准确表示出∠COM与∠CON的度数是解题的关键,此题规律性较强,是不错的好题.
∴∠COM=
 ∠BOC=
∠BOC= ×120°=60°,
×120°=60°,∵ON平分∠AOC,
∴∠CON=
 ∠AOC=
∠AOC= ×30°=15°,
×30°=15°,∴∠MON=∠COM-∠CON=60°-15°=45°;
(2)∵∠BOC=∠AOB+∠AOC=90°+20°=110°,射线OM平分∠BOC,
∴∠COM=
 ∠BOC=
∠BOC= ×110°=55°,
×110°=55°,∵ON平分∠AOC,
∴∠CON=
 ∠AOC=
∠AOC= ×20°=10°,
×20°=10°,∴∠MON=∠COM-∠CON=55°-10°=45°;
(3)∵∠BOC=∠AOB+∠AOC=90°+α,射线OM平分∠BOC,
∴∠COM=
 ∠BOC=
∠BOC= ×(90°+α),
×(90°+α),∵ON平分∠AOC,
∴∠CON=
 ∠AOC=
∠AOC= α,
α,∴∠MON=∠COM-∠CON=
 ×(90°+α)-
×(90°+α)- α=45°+
α=45°+ α-
α- α=45°;
α=45°;(4))∵∠BOC=∠AOB+∠AOC=β+30°,射线OM平分∠BOC,
∴∠COM=
 ∠BOC=
∠BOC= (β+30°),
(β+30°),∵ON平分∠AOC,
∴∠CON=
 ∠AOC=
∠AOC= ×30°=15°,
×30°=15°,∴∠MON=∠COM-∠CON=
 (β+30°)-15°=
(β+30°)-15°= β+15°-15°=
β+15°-15°= β.
β.分析:(1)根据三角板的度数求出∠BOC的度数,再根据角平分线的定义求出∠COM与∠CON的度数,然后根据∠MON=∠COM-∠CON,代入数据进行计算即可得解;
(2)先求出∠BOC的度数,再根据角平分线的定义求出∠COM与∠CON的度数,然后根据∠MON=∠COM-∠CON,代入数据进行计算即可得解;
(3)∠BOC的度数,再根据角平分线的定义求出∠COM与∠CON的度数,然后根据∠MON=∠COM-∠CON,代入数据进行计算即可得解;
(4)∠BOC的度数,再根据角平分线的定义求出∠COM与∠CON的度数,然后根据∠MON=∠COM-∠CON,代入数据进行计算即可得解;
点评:本题考查了角的计算以及旋转的性质,认准图形,准确表示出∠COM与∠CON的度数是解题的关键,此题规律性较强,是不错的好题.

练习册系列答案
相关题目
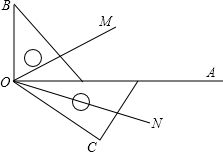 如图,两块三角板摆放在一起,射线OM平分∠BOC、ON平分∠AOC.
如图,两块三角板摆放在一起,射线OM平分∠BOC、ON平分∠AOC.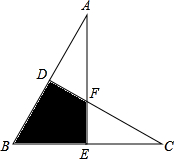 将两块大小完全相同的直角三角板△AEB和△CDB如图摆放,斜边AB=BC=10cm,∠B=60°.求图中两块三角板重叠部分(即四边形DBEF)的面积.
将两块大小完全相同的直角三角板△AEB和△CDB如图摆放,斜边AB=BC=10cm,∠B=60°.求图中两块三角板重叠部分(即四边形DBEF)的面积. 将两块大小完全相同的直角三角板△AEB和△CDB如图摆放,斜边AB=BC=10cm,∠B=60°.求图中两块三角板重叠部分(即四边形DBEF)的面积.
将两块大小完全相同的直角三角板△AEB和△CDB如图摆放,斜边AB=BC=10cm,∠B=60°.求图中两块三角板重叠部分(即四边形DBEF)的面积.