题目内容
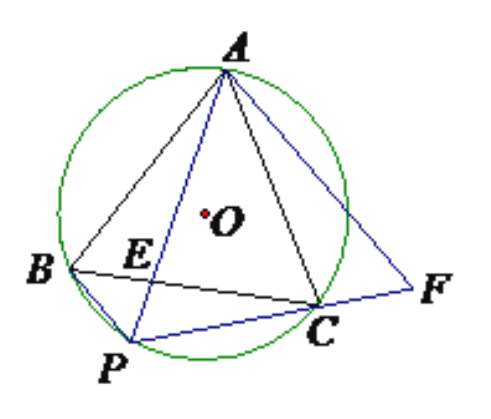
【题目】如图,正三角形ABC内接于⊙O,P是BC上的一点,且PB<PC,PA交BC于E,点F是PC延长线上的点,CF=PB,AB=![]() ,PA=4.
,PA=4.
(1)求证:△ABP≌△ACF;
(2)求证:AC2=PAAE;
(3)求PB和PC的长.

【答案】(1)证明见解析;(2)证明见解析;(3)PB=1,PC=3.
【解析】试题分析:(1)先根据等边三角形的性质得到AB=AC,再利用圆的内接四边形的性质得∠ACF=∠ABP,于是可根据“SAS”判断△ABP≌△ACF;
(2)先根据等边三角形的性质得到∠ABC=∠ACB=60°,再根据圆周角定理得∠APC=∠ABB=60°,加上∠CAE=∠PAC,于是可判断△ACE∽△APC,然后利用相似比即可得到结论;
(3)先利用AC2=PAAE计算出AE=![]() ,则PE=AP-AE=
,则PE=AP-AE=![]() ,再证△APF为等边三角形,得到PF=PA=4,则有PC+PB=4,接着证明△ABP∽△CEP,得到PBPC=PEA=3,然后根据根与系数的关系,可把PB和PC看作方程x2-4x+3=0的两实数解,再解此方程即可得到PB和PC的长.
,再证△APF为等边三角形,得到PF=PA=4,则有PC+PB=4,接着证明△ABP∽△CEP,得到PBPC=PEA=3,然后根据根与系数的关系,可把PB和PC看作方程x2-4x+3=0的两实数解,再解此方程即可得到PB和PC的长.
试题解析:
(1)∵∠ACP+∠ABP=180°,
又∠ACP+∠ACF=180°,
∴∠ABP=∠ACF
在![]() 和
和![]() 中,
中,
∵AB=AC,∠ABP=∠ACF, ![]()
∴![]() ≌
≌![]() .
.
(2)在![]() 和
和![]() 中,
中,
∵∠APC=∠ABC,
而![]() 是等边三角形,故∠ACB=∠ABC=60,
是等边三角形,故∠ACB=∠ABC=60,
∴∠ACE =∠APC .
又∠CAE =∠PAC ,
∴![]() ∽
∽![]()
∴![]() ,即
,即![]() .
.
由(1)知![]() ≌
≌![]() ,
,
∴∠BAP=∠CAF, ![]()
∴∠BAP+∠PAC=∠CAF+∠PAC
∴∠PAF=∠BAC=60°,又∠APC=∠ABC=60°.
∴![]() 是等边三角形
是等边三角形
∴AP=PF
∴![]()
在![]() 与
与![]() 中,
中,
∵∠BAP=∠ECP ,
又∠APB=∠EPC=60°,
∴![]() ∽
∽![]()
∴![]() ,即
,即![]()
由(2)![]() ,
,
∴![]()
∴![]()
∴![]()
因此PB和PC的长是方程![]() 的解.
的解.
解这个方程,得![]() ,
, ![]() .
.
∵PB<PB,∴PB=![]() ,PC=
,PC=![]() ,
,
∴PB和PC的长分别是1和3。