题目内容
15.已知等式$\frac{\sqrt{{x}^{2}-6x+9}}{x-3}$+(x-3)2=0,则x=2.分析 由等式可知x-3≠0,按照x-3>0,x-3<0分类,将等式化简,解一元二次方程即可.
解答 解:∵x-3≠0,
①当x-3>0时,原等式整理得1+(x-3)2=0,一个正数加一个非负数不可能为0,这种情况不存在.
②当x-3<0,即x<3时,原等式整理得:-1+(x-3)2=0,则x-3=1或x-3=-1,
解得x=4或x=2,而x<3,所以,只有x=2符合条件.
故答案为:2.
点评 本题的难点在于判断第一项为1,还是-1,分情况讨论后,所得结果还应适合给定的范围.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
5.不为0的四个实数a、b,c、d满足ab=cd,改写成比例式错误的是( )
| A. | $\frac{a}{c}$=$\frac{d}{b}$ | B. | $\frac{c}{a}$=$\frac{b}{d}$ | C. | $\frac{d}{a}$=$\frac{b}{c}$ | D. | $\frac{a}{b}$=$\frac{c}{d}$ |
20.-2015的相反数是( )
| A. | 2015 | B. | $\frac{1}{2015}$ | C. | -$\frac{1}{2015}$ | D. | -2015 |
7.测定某运动员跑100m的平均速度,测的结果是跑完前24m用了3s,跑完后76m又用了6s,该运动员的平均速度是( )
| A. | 8m/s | B. | 11.1m/s | C. | 12.7m/s | D. | 10.35m/s |
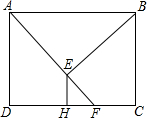 如图,矩形ABCD中,F为CD边上一点,AF=AB,BE⊥AF,EH⊥CD垂足分别为点E、H.
如图,矩形ABCD中,F为CD边上一点,AF=AB,BE⊥AF,EH⊥CD垂足分别为点E、H.