题目内容
【题目】如图,△ABC中,E为AD与CF的交点,AE=ED,已知△ABC的面积是1,△BEF的面积是 ![]() ,则△AEF的面积是;
,则△AEF的面积是;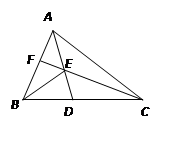
【答案】![]()
【解析】解:作AM⊥BC于M,EN⊥BC于N,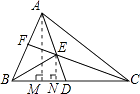
则EN∥AM,ED:AD=EN:AM,
∵AE=ED,
∴AD=2AE,
∴AM=2EN,
作AM⊥BC于M,EN⊥BC于N,得出EN∥AM,
∴S△ABC= ![]() BCAM,S△EBC=
BCAM,S△EBC= ![]() BCEN,
BCEN,
∴S△EBC= ![]() S△ABC又∵S△BEF=
S△ABC又∵S△BEF= ![]()
∴S△FBC=S△EBC+S△BEF= ![]() +
+ ![]() =
= ![]()
∴S△AFC=S△ABC-S△FBC=1- ![]() =
= ![]()
分别将AF和BF看做S△AFC和S△FBC的底,由于两个三角形的高相同,
∴AF:FB=S△AFC:S△FBC= ![]() :
: ![]() =2:3
=2:3
,
分别将AF和BF看做S△AFE和S△FBE的底,由于两个三角形的高相同
∴S△AFE:S△BEF=AF:FB=2:3,
∴S△AFE= ![]() ×
× ![]() =
= ![]()
根据平行线分线段成比例及线段中点的定义证得AM=2EN,可得到△EBC的面积等于△ABC面积的一半,再根据S△FBC=S△EBC+S△BEF及△ABC的面积是1,△BEF的面积是 ![]() , 求出△FBC的面积,再根据S△AFC=S△ABC-S△FBC , 就可求出△AFC的面积,然后根据S△AFC和S△FBC两个三角形的高相同,求出底边之比,根据S△AFE:S△BEF=AF:FB=2:3,即可求出答案。
, 求出△FBC的面积,再根据S△AFC=S△ABC-S△FBC , 就可求出△AFC的面积,然后根据S△AFC和S△FBC两个三角形的高相同,求出底边之比,根据S△AFE:S△BEF=AF:FB=2:3,即可求出答案。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目