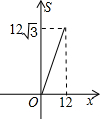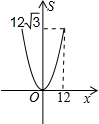题目内容
有正三角形ABC，边长为2．D、E分别是AB、AC的中点，则梯形BCED面积为
- A.
- B.
- C.
- D.
C
分析：根据△ADE为等边三角形，且边长为1，求EF，根据EF，AD计算△ADE的面积，同理计算△ABC的面积，根据梯形BCED的面积为△ABC的面积减去△ADE的面积，即可求得梯形BCED的面积．
解答：
解：作EF⊥AD于点F，AH⊥BC于点H，
∵D、E为AB、AC的中点
∴DE=
BC=1，且AD=AE=1，
∴△ADE亦为等边三角形，
∴AF=AD=，
∴EF=
=，
同理AH=，
∴△ADE面积为：×EF×AD=×1×=，
∵△ABC面积为：×BC×AH=×2×=，
∴梯形BCED的面积为-=．
故选：C．
点评：本题考查了勾股定理的灵活运用，考查了正三角形面积的计算，正确计算△ABC和△ADE的面积值是解题的关键．
分析：根据△ADE为等边三角形，且边长为1，求EF，根据EF，AD计算△ADE的面积，同理计算△ABC的面积，根据梯形BCED的面积为△ABC的面积减去△ADE的面积，即可求得梯形BCED的面积．
解答：
解：作EF⊥AD于点F，AH⊥BC于点H，∵D、E为AB、AC的中点
∴DE=
BC=1，且AD=AE=1，∴△ADE亦为等边三角形，
∴AF=
AD=，∴EF=
=，同理AH=
，∴△ADE面积为：
×EF×AD=×1×=，∵△ABC面积为：
×BC×AH=×2×=，∴梯形BCED的面积为
-=．故选：C．
点评：本题考查了勾股定理的灵活运用，考查了正三角形面积的计算，正确计算△ABC和△ADE的面积值是解题的关键．
练习册系列答案
相关题目
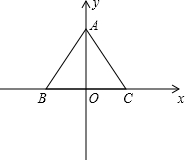如图，坐标平面中有一正三角形ABC，边长为2，
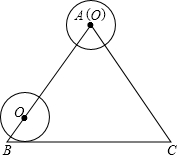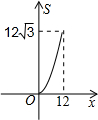
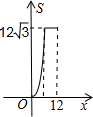
-BC-CA运动，回到点A时，⊙O随着点O的运动而移动．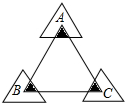
如图，正三角形ABC的边长为12，三个全等的小正三角形重心（即三条中线的交点）与正三角形ABC的顶点重合，且他们各有一边与正三角形ABC的一边平行．若小正三角形的边长为x，且0＜x≤12，阴影部分的面积为S，则能反映S与x之间函数关系的大致图象是（ ）
