题目内容
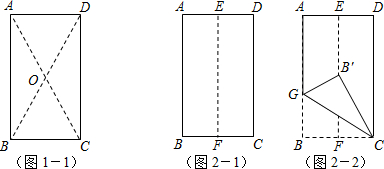
 如图点P是矩形ABCD的边AD上的任一点,AB=8,BC=15,则点P到矩形的两条对角线AC和BD的距离之和是
如图点P是矩形ABCD的边AD上的任一点,AB=8,BC=15,则点P到矩形的两条对角线AC和BD的距离之和是分析:由矩形ABCD可得:S△AOD=
S矩形ABCD,又由AB=8,BC=15,可求得AC的长,则可求得OA与OD的长,又由S△AOD=S△APO+S△DPO=
OA•PE+
OD•PF,代入数值即可求得结果.
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:过点P作PE⊥AC于E,PF⊥BD与F,连接OP,
解:过点P作PE⊥AC于E,PF⊥BD与F,连接OP,
∵四边形ABCD是矩形,
∴AC=BD,OA=OC=
AC,OB=OD=
BD,∠ABC=90°,
S△AOD=
S矩形ABCD,
∴OA=OD=
AC,
∵AB=8,BC=15,
∴AC=
=
=17,S△AOD=
S矩形ABCD=30,
∴OA=OD=
,
∴S△AOD=S△APO+S△DPO=
OA•PE+
OD•PF=
OA•(PE+PF)=
×
(PE+PF)=30,
∴PE+PF=
.
∴点P到矩形的两条对角线AC和BD的距离之和是
.
故答案为:
.
 解:过点P作PE⊥AC于E,PF⊥BD与F,连接OP,
解:过点P作PE⊥AC于E,PF⊥BD与F,连接OP,∵四边形ABCD是矩形,
∴AC=BD,OA=OC=
| 1 |
| 2 |
| 1 |
| 2 |
S△AOD=
| 1 |
| 4 |
∴OA=OD=
| 1 |
| 2 |
∵AB=8,BC=15,
∴AC=
| AB2+BC2 |
| 289 |
| 1 |
| 4 |
∴OA=OD=
| 17 |
| 2 |
∴S△AOD=S△APO+S△DPO=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 17 |
| 2 |
∴PE+PF=
| 120 |
| 17 |
∴点P到矩形的两条对角线AC和BD的距离之和是
| 120 |
| 17 |
故答案为:
| 120 |
| 17 |
点评:此题考查了矩形的性质.解此题的关键是将△AOD的面积用矩形求得,再用△APO与△POD的面积和表示出来.还要注意数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目