题目内容
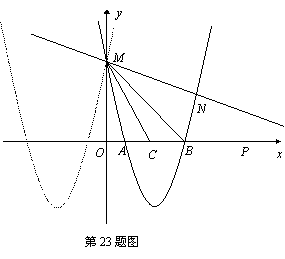
如图,已知抛物线![]() 与
与![]() 关于y轴对称,与y轴交于点M,与x轴交于点A和B.
关于y轴对称,与y轴交于点M,与x轴交于点A和B.
(1)求出![]() 的解析式,试猜想出与一般形式抛物线
的解析式,试猜想出与一般形式抛物线![]() 关于y轴对称的二次函数解析式(不要求证明).
关于y轴对称的二次函数解析式(不要求证明).
(2)若A,B的中点是点C,求sin∠CMB.
(3)如果过点M的一条直线与![]() 图象相交于另一点N(a,b),a
图象相交于另一点N(a,b),a![]() b且满足a2-a+q=0,b2-b+q=0(q为常数),求点N的坐标.
b且满足a2-a+q=0,b2-b+q=0(q为常数),求点N的坐标.
 |
解:(1)![]() 的顶点为(-3,-4),
的顶点为(-3,-4),
即![]() 的顶点的为(3,-4),
的顶点的为(3,-4),
即![]() ,
,
![]() 与y轴的交点M(0,5),
与y轴的交点M(0,5),
即![]() 与y轴的交点M(0,5).
与y轴的交点M(0,5).
即a=1,所求二次函数为![]()
猜想:与一般形式抛物线![]() 关于y
关于y
轴对称的二次函数解析式是![]() .
.
 |
(2)过点C作CD⊥BM于D.
抛物线![]() 与x轴的交点A(1,0),
与x轴的交点A(1,0),
B(5,0),与y轴交点M(0,5),AB中点C
(3,0);故△MOB,△BCD是等腰直角三角形,
CD![]() ,BC=2. 在Rt△MOC中,MC=
,BC=2. 在Rt△MOC中,MC=![]() .
.
则sin∠CMB=![]() .
.
(3)设过点M(0,5)的直线为y=kx+5
![]() 解得
解得![]()
![]()
则a=k+6,b=k2+6x+5.
由已知a,b是方程x2-x+9=0的两个根,
故a+b=1.(k+6)+(k2+6k+5)=1,
化k2+7k+10=0,则k1=-2,k2=-5.
点N的坐标是(4,-3)或(1,0).

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
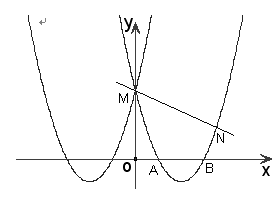
 与
与 关于
关于 轴对称,并与
轴对称,并与 轴交于点A和B.
轴交于点A和B.
 关于
关于 ;
;  过点
过点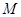 ,且与抛物线
,且与抛物线 ,相交于另一点
,相交于另一点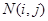 ,如果
,如果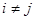 ,且
,且
 ,求
,求 的值。
的值。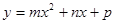 与
与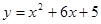 关于
关于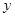 轴对称,并与
轴对称,并与 轴交于点A和B.
轴交于点A和B.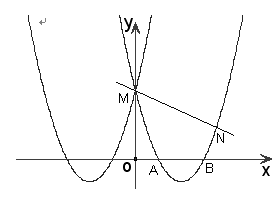
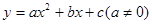 关于
关于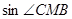 ;
; 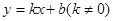 过点
过点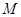 ,且与抛物线
,且与抛物线 ,相交于另一点
,相交于另一点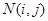 ,如果
,如果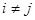 ,且
,且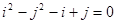
 ,求
,求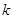 的值。
的值。 与
与 关于
关于 轴对称,并与
轴对称,并与 轴交于点A和B.
轴交于点A和B.
 关于
关于 ;
;
 过点
过点 ,且与抛物线
,且与抛物线 ,如果
,如果 ,且
,且
 ,求
,求 的值。
的值。