题目内容
 如图,有两棵树高分别为6米、2米,它们相距5米,一只小鸟从一棵树的树梢飞到另一棵树的树梢,一共飞了多少米?( )
如图,有两棵树高分别为6米、2米,它们相距5米,一只小鸟从一棵树的树梢飞到另一棵树的树梢,一共飞了多少米?( )| A、41 | ||
B、
| ||
| C、3 | ||
| D、9 |
分析:过D作DE⊥AB交AB与E点,则:由题给图形可得,四边形CDEB为矩形,三角形AED为直角三角形,再由矩形的性质可知AE、ED的长,最后运用勾股定理解直角三角形,即可得出AD的长.
解答:解:如下图所示,作DE⊥AB交AB与E点,则:
四边形CDEB为矩形,三角形AED为直角三角形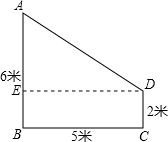
已知,AB=6,BC=5,CD=2,
∴BE=2,DE=5,
∴AE=AB-BE=4,
在直角三角形AED中,
由勾股定理可得:
AD2=AE2+ED2
∴AD=
=
故选B.
四边形CDEB为矩形,三角形AED为直角三角形

已知,AB=6,BC=5,CD=2,
∴BE=2,DE=5,
∴AE=AB-BE=4,
在直角三角形AED中,
由勾股定理可得:
AD2=AE2+ED2
∴AD=
| 42+ 52 |
| 41 |
故选B.
点评:本题考查了矩形的性质及运用勾股定理解直角三角形.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 如图,有两棵树高分别为6米、2米,它们相距5米,一只小鸟从一棵树的树梢飞到另一棵树的树梢,一共飞了多少米?
如图,有两棵树高分别为6米、2米,它们相距5米,一只小鸟从一棵树的树梢飞到另一棵树的树梢,一共飞了多少米?

