题目内容
 如图,在Rt△ABC中,∠A=90°,AB=AC=4
如图,在Rt△ABC中,∠A=90°,AB=AC=4 ,点D为AC的中点,点E在边BC上,且ED⊥BD,则△CDE的面积是________.
,点D为AC的中点,点E在边BC上,且ED⊥BD,则△CDE的面积是________.
2
分析:先根据点D为AC的中点,求出S△ABD=S△BDC= S△ABC=12,然后过D点作DF垂直于BC于F点,求出DF,再利用勾股定理和射影定理求出BF和BE,然后即可求出CE,那么就可以求出△CDE的面积了.
S△ABC=12,然后过D点作DF垂直于BC于F点,求出DF,再利用勾股定理和射影定理求出BF和BE,然后即可求出CE,那么就可以求出△CDE的面积了.
解答: 解:点D为AC的中点
解:点D为AC的中点
故AD=DC= AC=2
AC=2 ,
,
S△ABD=S△BDC= S△ABC=12,
S△ABC=12,
由勾股定理得BC= =4
=4 ,
,
过D点作DF垂直于BC于F点,
DF= =
= =
= ,
,
BD2=AD2+AB2=12+48=60,
BD=2 ,
,
由勾股定理得BF= =
=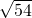 =3
=3 ,
,
由射影定理得BD2=BF•BE,
∴BE= =
= =
=
CE=BC-BE=4 -
- =
= ,
,
S△CDE= ×CE×DF=
×CE×DF= ×
× ×
× =2.
=2.
故答案为:2.
点评:此题考查学生对勾股定理,三角形面积、射影定理等知识点的理解和掌握,综合性较强,有一定难度,属于难题.
分析:先根据点D为AC的中点,求出S△ABD=S△BDC=
 S△ABC=12,然后过D点作DF垂直于BC于F点,求出DF,再利用勾股定理和射影定理求出BF和BE,然后即可求出CE,那么就可以求出△CDE的面积了.
S△ABC=12,然后过D点作DF垂直于BC于F点,求出DF,再利用勾股定理和射影定理求出BF和BE,然后即可求出CE,那么就可以求出△CDE的面积了.解答:
 解:点D为AC的中点
解:点D为AC的中点故AD=DC=
 AC=2
AC=2 ,
,S△ABD=S△BDC=
 S△ABC=12,
S△ABC=12,由勾股定理得BC=
 =4
=4 ,
,过D点作DF垂直于BC于F点,
DF=
 =
= =
= ,
,BD2=AD2+AB2=12+48=60,
BD=2
 ,
,由勾股定理得BF=
 =
=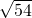 =3
=3 ,
,由射影定理得BD2=BF•BE,
∴BE=
 =
= =
=
CE=BC-BE=4
 -
- =
= ,
,S△CDE=
 ×CE×DF=
×CE×DF= ×
× ×
× =2.
=2.故答案为:2.
点评:此题考查学生对勾股定理,三角形面积、射影定理等知识点的理解和掌握,综合性较强,有一定难度,属于难题.

练习册系列答案
相关题目
 (2013•莆田质检)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,点E是AB上一点,以AE为直径的⊙O过点D,且交AC于点F.
(2013•莆田质检)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,点E是AB上一点,以AE为直径的⊙O过点D,且交AC于点F. 如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,AD和BD分别是∠BAC和∠ABC的平分线,它们相交于点D,求点D到BC的距离.
如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,AD和BD分别是∠BAC和∠ABC的平分线,它们相交于点D,求点D到BC的距离. 边上移动,使这个30°角的两边分别与△ABC的边AC、BC相交于点E、F,且使DE始终与AB垂直.
边上移动,使这个30°角的两边分别与△ABC的边AC、BC相交于点E、F,且使DE始终与AB垂直. 如图,在Rt△ABC中,BD⊥AC,sinA=
如图,在Rt△ABC中,BD⊥AC,sinA= 点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s).
点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s).