Question

（本题满分12分）一家计算机专买店A型计算器每只进价12元，售价20元，多买优惠：凡是一次买10只以上的，每多买一只，所买的全部计算器每只就降低0.10元，例如，某人买20只计算器，于是每只降价0.10×（20-10）＝1（元），因此，所买的全部20只计算器都按每只19元的价格购买．但是最低价为每只16元．
【小题1】（1）求一次至少买多少只，才能以最低价购买？
【小题2】（2）写出专买店当一次销售x（x＞10）只时，所获利润y元）与x（只）之间的函数关系式，并写出自变量x的取值范围；
【小题3】（3）一天，甲买了46只，乙买了50只，店主却发现卖46只赚的钱反而比卖50只赚的钱多，你能用数学知识解释这一现象吗？为了不出现这种现象，在其他优惠条件不变的情况下，店家应把最低价每只16元至少提高到多少？

Answer 1

【小题1】解：（1）设一次购买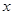只，则20－16，解得．
∴一次至少买50只，才能以最低价购买．……………… 4分
【小题2】（2）当时，    …… 6分
当时，．          …………………………8分
【小题3】（3）．[来源:Z_xx_k.Com]
①当10＜x≤45时，随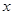的增大而增大，即当卖的只数越多时，利润更大．
②当45＜x≤50时，随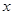的增大而减小，即当卖的只数越多时，利润变小．
且当时，y₁=202.4，
当时，y₂=200． ……………………………………………10分
y₁＞y₂．
即出现了卖46只赚的钱比卖50只嫌的钱多的现象．
当时，最低售价为（元）．  
∴为了不出现这种现象，在其他优惠条件不变的情况下，店家应把最低价每只16元至少提高到16.5元 .               ………………………12分

解析