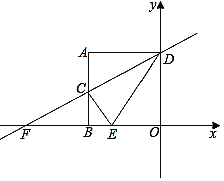
��Ŀ����
����Ŀ����ͼ��������y=x2+bx+c��x�ύ��A��B���㣬B������Ϊ��4��0������y�ύ�ڵ�C��0��4����
��1���������ߵĽ���ʽ��
��2����P��x���·����������ϣ�����P��ֱ��y=x+m��ֱ��BC���ڵ�E����y�ύ�ڵ�F����PE+EF�����ֵ��
��3����DΪ�����߶Գ�����һ�㣮
�ٵ���BCD����BCΪֱ�DZߵ�ֱ��������ʱ��ֱ��д����D�����ꣻ
������BCD����������Σ�ֱ��д����D��������n��ȡֵ��Χ��

���𰸡���1�������ߵĽ���ʽΪy=x2��5x+4����2��PE+EF�����ֵΪ![]() ����3���ٷ��������ĵ�D�������ǣ�
����3���ٷ��������ĵ�D�������ǣ�![]() ��
��![]() ����
����![]() ����
����![]() �����ڵ�D���������ȡֵ��ΧΪ
�����ڵ�D���������ȡֵ��ΧΪ![]() ��y��
��y��![]() ��
��![]() ��y��
��y��![]() ��
��
����������1�����ô���ϵ�����������ߵĽ���ʽ��
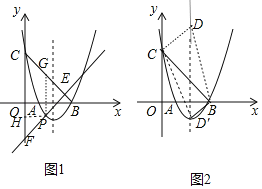
��2����BC�Ľ���ʽΪy=��x+4����֤����ECFΪ����ֱ�������Σ���PH��y����H��PG��y�ύBC��G����ͼ1������EPGΪ����ֱ�������Σ�PE=![]() PG����P��t��t2��4t+3����1��t��3������G��t����t+3������������t��ʾPF��PE������PE+EF=2PE+PF=��
PG����P��t��t2��4t+3����1��t��3������G��t����t+3������������t��ʾPF��PE������PE+EF=2PE+PF=��![]() t2+5
t2+5![]() t��Ȼ�����ö��κ��������ʽ�����⣻
t��Ȼ�����ö��κ��������ʽ�����⣻
��3������ͼ2�������ߵĶԳ���Ϊֱ��x=����D���������ȡֵ��Χ��
��������BCD����BCΪб�ߵ�ֱ����������4+��y��3��2+1+y2=18�����y1=![]() ��y2=
��y2=![]() ���õ���ʱD������Ϊ��
���õ���ʱD������Ϊ��![]() ��
��![]() ����
����![]() ��
��![]() ����Ȼ����ͼ�ο�ȷ����BCD�����������ʱ��D���������ȡֵ��Χ��
����Ȼ����ͼ�ο�ȷ����BCD�����������ʱ��D���������ȡֵ��Χ��
��1����B��4��0����C��0��4������y=x2+bx+c����
![]() ��
��
��� ![]() ��
��
�������ߵĽ���ʽΪy=x2��5x+4��
��2����B��4��0����C��0��4�������ݴ���ϵ������BC�Ľ���ʽΪy=��x+4��
��ֱ��y=x+m��ֱ��y=xƽ�У�
��ֱ��y=��x+4��ֱ��y=x+m��ֱ��
���CEF=90�㣬
���ECFΪ����ֱ�������Σ�
��PH��y����H��PG��y�ύBC��G����ͼ1����EPGΪ����ֱ�������Σ�PE=![]() PG��
PG��
��P��t��t2��5t+4����1��t��4������G��t����t+4����
��PF=![]() PH=
PH=![]() t��PG=��t+4����t2��5t+4��=��t2+4t��
t��PG=��t+4����t2��5t+4��=��t2+4t��
��PE=![]() PG=��
PG=��![]() t2+2
t2+2![]() t��
t��
��PE+EF=PE+PE+PF=2PE+PF=��![]() t2+4
t2+4![]() t+
t+![]() t=��
t=��![]() t2+5
t2+5![]() t=��
t=��![]() ��t��
��t��![]() ��2+
��2+![]() ��
��
��t=![]() ʱ��PE+EF�����ֵΪ
ʱ��PE+EF�����ֵΪ![]() ��
��
��3������ͼ2�������ߵĶԳ���Ϊֱ��x=![]() ��
��
��D��![]() ��y������BC2=42+42=32��DC2=��
��y������BC2=42+42=32��DC2=��![]() ��2+��y��4��2��BD2=��4��
��2+��y��4��2��BD2=��4��![]() ��2+y2=
��2+y2=![]() +y2��
+y2��
����BCD����BCΪֱ�DZߣ�BDΪб�ߵ�ֱ��������ʱ��BC2+DC2=BD2��
��32+��![]() ��2+��y��4��2=
��2+��y��4��2=![]() +y2�����y=5����ʱD������Ϊ��
+y2�����y=5����ʱD������Ϊ��![]() ��
��![]() ����
����
����BCD����BCΪֱ�DZߣ�CDΪб�ߵ�ֱ��������ʱ��BC2+DB2=DC2��
��32+![]() +y2=��
+y2=��![]() ��2+��y��4��2�����y=��1����ʱD������Ϊ��
��2+��y��4��2�����y=��1����ʱD������Ϊ��![]() ����
����![]() ����
����
�������������������ĵ�D�������ǣ�![]() ��
��![]() ����
����![]() ����
����![]() ����
����
�ڵ���BCD����BCΪб�ߵ�ֱ��������ʱ��DC2+DB2=BC2������![]() ��2+��y��4��2+
��2+��y��4��2+![]() +y2=32�����y1=
+y2=32�����y1=![]() ��y2=
��y2=![]() ����ʱD������Ϊ��
����ʱD������Ϊ��![]() ��
��![]() ����
����![]() ��
��![]() ����
����
������BCD����������Σ���D���������ȡֵ��ΧΪ![]() ��y��
��y��![]() ��
��![]() ��y��
��y��![]() ��
��

 ��Կ���Ծ�ϵ�д�
��Կ���Ծ�ϵ�д�