题目内容
在同一平面坐标系中,函数y=mx+m和y=﹣mx2+2x+2(m是常数,且m≠0)的图象可能是( )
A. 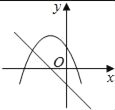 B.
B. 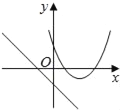 C.
C. 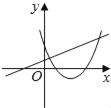 D.
D. 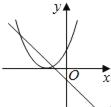
【答案】D
【解析】A.由函数y=mx+m的图象可知m<0,即函数y=?mx2+2x+2开口方向朝上,与图象不符,故A选项错误;
B.由函数y=mx+m的图象可知m<0,对称轴为x=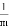 <0,则对称轴应在y轴左侧,与图象不符,故B选项错误;
<0,则对称轴应在y轴左侧,与图象不符,故B选项错误;
C.由函数y=mx+m的图象可知m>0,即函数y=?mx2+2x+2开口方向朝下,与图象不符,故C选项错误;
D.由函数y=mx+m的图象可知m<0,即函数y=?mx2+2x+2开口方向朝上,对称轴为x=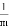 <0,则对称轴应在y轴左侧,与图象相符,故D选项正确;
<0,则对称轴应在y轴左侧,与图象相符,故D选项正确;
故选:D.
【题型】单选题
【结束】
10
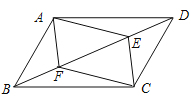
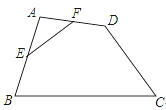
如图,已知菱形ABCD的周长为16,面积为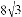 ,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为( )
,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为( )
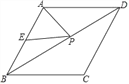
A. 2 B. 2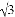 C. 4 D. 4
C. 4 D. 4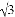
练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目





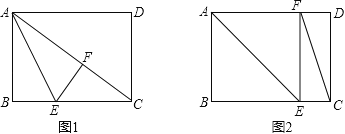
 =45°;
=45°;
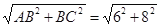 =10,
=10,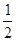 ×90°=45°,
×90°=45°, )﹣2﹣
)﹣2﹣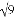 +(
+(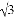 ﹣4)0﹣
﹣4)0﹣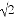 cos45°.
cos45°.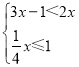 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )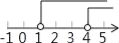 B.
B.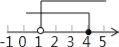
 D.
D.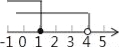
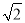 +
+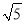 =
=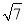 B. 3
B. 3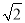 ﹣
﹣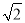 =3 C.
=3 C. 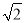 ×
×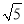 =
=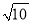 D.
D. 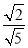 =5
=5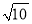
 B.
B.  C.
C.  D.
D. 