题目内容
解方程组
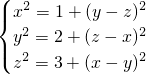 .
.
解:∵x2=1+(y-z)2,
∴x2-(y-z)2=1,
∴(x+y-z)(x-y+z)=1,(I)
同理y2=2+(z-x)2推出(y+z-x)(y-z+x)=2,(II)
同理z2=3+(x-y)2推出(z+x-y)(z-x+y)=3,(III)
设x+y-z=a,x-y+z=b,z-x+y=c,
则原方程组变形为: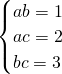 ,
,
解得: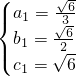 ,
,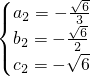 ,
,
即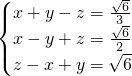 或
或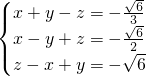
解得: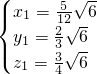 ,
,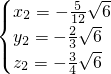 .
.
分析:先变形得出(x+y-z)(x-y+z)=1,(y+z-x)(y-z+x)=2,(z+x-y)(z-x+y)=3,设x+y-z=a,x-y+z=b,z-x+y=c,
得出新方程组,求出a b c的值,再代入求出即可.
点评:本题考查了解高次方程组的应用,用了换元法,题目比较好,但难度偏大.
∴x2-(y-z)2=1,
∴(x+y-z)(x-y+z)=1,(I)
同理y2=2+(z-x)2推出(y+z-x)(y-z+x)=2,(II)
同理z2=3+(x-y)2推出(z+x-y)(z-x+y)=3,(III)
设x+y-z=a,x-y+z=b,z-x+y=c,
则原方程组变形为:
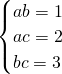 ,
,解得:
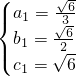 ,
,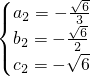 ,
,即
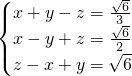 或
或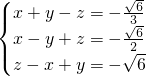
解得:
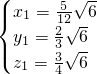 ,
,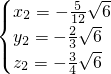 .
.分析:先变形得出(x+y-z)(x-y+z)=1,(y+z-x)(y-z+x)=2,(z+x-y)(z-x+y)=3,设x+y-z=a,x-y+z=b,z-x+y=c,
得出新方程组,求出a b c的值,再代入求出即可.
点评:本题考查了解高次方程组的应用,用了换元法,题目比较好,但难度偏大.

练习册系列答案
相关题目
 (1)解方程组:
(1)解方程组: