题目内容
【题目】如图,在平面直角坐标系中,A(-4,0)、B(2,0),点C在y轴的正半轴上,且三角形ABC的面积为![]() .
.
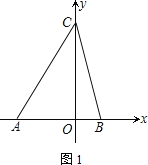
(1)求点C的坐标.
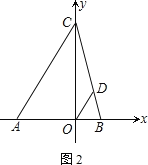
(2)过O点作OD平行于AC交CB于点D,问:x轴上是否存在一点P,使S△PBD=![]() ?若存在,求出点P的坐标;若不存在,请说明理由.
?若存在,求出点P的坐标;若不存在,请说明理由.
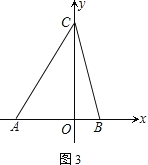
(3)若∠ACO=30°,射线CA绕C点以每秒3°的速度逆时针旋转到CA′,射线OB绕O点以每秒10°的速度逆时针旋转到OB′.当OB转动一周时两者都停止运动.若两射线同时开始运动,在旋转过程中,经过多长时间,CA′∥OB′?
【答案】(1)C(0,![]() )(2)(-7,0)或(11,0)(3)
)(2)(-7,0)或(11,0)(3)![]() s或
s或![]() s
s
【解析】
(1)根据三角形的面积公式即可求解;
(2)先得到直线AC与BC的解析式,再根据平行得到OD解析式,再联立解得D点坐标,再根据S△PBD=![]() 即可求出P点坐标,
即可求出P点坐标,
(3)设旋转的时间为t,根据平行线的性质及角度的旋转即可得到一元一次方程,即可求解.
(1)∵A(-4,0)、B(2,0)
∴AB=6,
∵S△ABC=![]() AB×OC=
AB×OC=![]()
∴OC=![]()
∴C(0,![]() )
)
(2)∵A(-4,0)、C(0,![]() )
)
设直线AC解析式为y=kx+b(k≠0)
代入得 解得
解得
∴直线AC解析式为y=![]() x+4
x+4![]() ,
,
∵AC∥OD,∴OD解析式为y=![]() x
x
又B(2,0),可求得直线BC的解析式为y=-2![]() x+4
x+4![]()
联立y=![]() x与y=-2
x与y=-2![]() x+4
x+4![]()
解得x=![]() ,y=
,y=![]()
![]()
过D点作DF⊥x轴,∴DF=![]()
![]()
∵S△PBD=![]()
∴![]() BP×DF=
BP×DF=![]() ,即
,即![]() BP×
BP×![]()
![]() =
=![]() ,
,
BP=9,又B(2,0)
∴P点坐标为(-7,0)或(11,0)

(3)设旋转的时间为t,
∵每秒10°的速度逆时针旋转到OB′.当OB转动一周时两者都停止运动
∴10t≤360,则t≤36
依题意可得3x-30°=10x-90°或30-2x=90°-10x-180°
解得x=![]() ,x=
,x=![]()
故经过![]() s或
s或![]() s,CA′∥OB′.
s,CA′∥OB′.

 阅读快车系列答案
阅读快车系列答案【题目】随着教育教学改革的不断深入,应试教育向素质教育转轨的力度不断加大,体育中考已成为初中毕业升学考试的重要内容之一。为了解某市九年级学生中考体育成绩情况,现从中随机抽取部分考生的体育成绩进行调查,并将调查结果绘制如下图表:
2019年中考体育成绩(分数段)统计表 | ||
分数段 | 频数(人) | 频率 |
25≤x<30 | 12 | 0.05 |
30≤x<35 | 24 | b |
35≤x<40 | 60 | 0.25 |
40≤x<45 | a | 0.45 |
45≤x<50 | 36 | 0.15 |
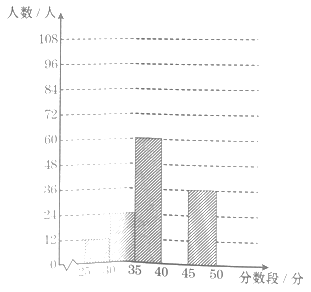
根据上面提供的信息,回答下列问题:
(1)表中a和b所表示的数分别为a=______,b=______;并补全频数分布直方图;
(2)甲同学说“我的体育成绩是此次抽样调查所得数据的中位数。”请问:甲同学的体育成绩在______分数段内?
(3)如果把成绩在40分以上(含40分)定为优秀那么该市12000名九年级考生中考体育成绩为优秀的约有多少名?