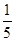题目内容
△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分为三个三角形,则S△ABO︰S△BCO︰S△CAO等于( )
A.1︰1︰1 B.1︰2︰3 C.2︰3︰4 D.3︰4︰5
A.1︰1︰1 B.1︰2︰3 C.2︰3︰4 D.3︰4︰5
C
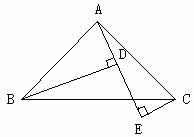
试题分析:首先过点O,作OD⊥AB于D,作OE⊥AC于E,作OF⊥BC于F,由点O是△ABC内角平分线的交点,根据角平分线的性质,即可得OD=OE=OF,继而可得
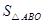 :
: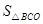 :
: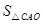 =AB:BC:CA,则可求得答案.
=AB:BC:CA,则可求得答案.过点O,作OD⊥AB于D,作OE⊥AC于E,作OF⊥BC于F,
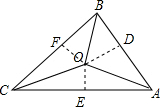
∵点O是△ABC内角平分线的交点,
∴OD=OE=OF,
∴
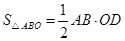 ,
,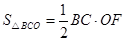 ,
,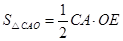 ,
,∵AB=20,BC=30,CA=40,
∴
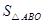 :
: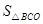 :
: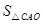 =AB:BC:CA =20:30:40=2:3:4.
=AB:BC:CA =20:30:40=2:3:4.故选C.
点评:解答本题的关键是掌握角平分线上的点到角的两边的距离相等,三角形三个内角平分线的交点到三边的距离相等。

练习册系列答案
相关题目
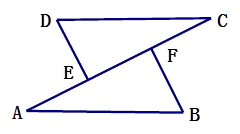
 是
是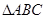 的一个外角,
的一个外角, 平分
平分 ,请问
,请问
 ㎝,则△ADE的周长是 。
㎝,则△ADE的周长是 。
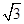 ,c=2
,c=2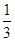 ,b=
,b=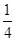 ,c=
,c=