题目内容
在如图所示的网格中,每个小方格的边长都是1。
(1)分别作出四边形ABCD关于y轴、原点的对称图形;
(2)以原点O为中心,将△ABD顺时针旋转90°,试画出旋转后的图形,并求旋转过程中△ABD扫过图形的面积。
(1)分别作出四边形ABCD关于y轴、原点的对称图形;
(2)以原点O为中心,将△ABD顺时针旋转90°,试画出旋转后的图形,并求旋转过程中△ABD扫过图形的面积。

解:
(1)所画图形如下图所示,
(2)如上图所示,△A′B′D′即为△ABD顺时针旋转90°后得到的图形,在旋转过程中可知:△ABD扫过图形的面积即是线段AB所扫过的扇环面积(S1)与△ABD的面积(S2)之和(S),
则有:S=S1+S2
=[ π×OA2﹣
π×OA2﹣ π×OB2]+
π×OB2]+ ×AD×1
×AD×1
=[ π×(22+42)﹣
π×(22+42)﹣ π×(12+12)]+
π×(12+12)]+ ×2×1
×2×1
= +1
+1
(1)所画图形如下图所示,

(2)如上图所示,△A′B′D′即为△ABD顺时针旋转90°后得到的图形,在旋转过程中可知:△ABD扫过图形的面积即是线段AB所扫过的扇环面积(S1)与△ABD的面积(S2)之和(S),
则有:S=S1+S2
=[
 π×OA2﹣
π×OA2﹣ π×OB2]+
π×OB2]+ ×AD×1
×AD×1=[
 π×(22+42)﹣
π×(22+42)﹣ π×(12+12)]+
π×(12+12)]+ ×2×1
×2×1=
 +1
+1
练习册系列答案
相关题目

 在如图所示的网格中,每个小正方形边长为1.
在如图所示的网格中,每个小正方形边长为1.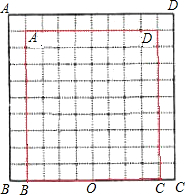 在如图所示的网格中,以BC的中点O为位似中心,把矩形ABCD缩小为原来的
在如图所示的网格中,以BC的中点O为位似中心,把矩形ABCD缩小为原来的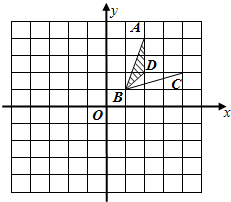 在如图所示的网格中,每个小方格的边长都是1.
在如图所示的网格中,每个小方格的边长都是1.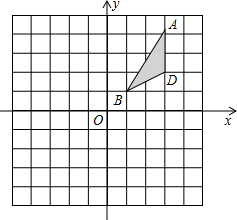 在如图所示的网格中,每个小方格的边长都是1.
在如图所示的网格中,每个小方格的边长都是1.