Question

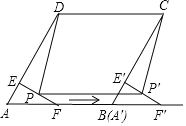
【题目】如图，在菱形ABCD中，∠A＝60°，AD＝8，F是AB的中点，过点F作FE⊥AD，垂足为E，将△AEF沿点A到点B的方向平移，得到△A′E′F′．

（1）求EF的长；

（2）设P，P′分别是EF，E′F′的中点，当点A′与点B重合时，求证四边形PP′CD是平行四边形，并求出四边形PP′CD的面积．

Answer 1

【答案】（1）2；（2）28.

【解析】

（1）首先求出AF的长度，再在直角三角形AEF中求出EF的长度；

（2）连接BD，DF，DF交PP′于H．首先证明四边形PP′CD是平行四边形，再证明DF⊥PP′，求出DH的长，最后根据面积公式求出答案．

（1）∵四边形ABCD是菱形，

∴AD＝AB＝8，

∵F是AB的中点，

∴AF＝AB＝×8＝4，

∵点F作FE⊥AD，∠A＝60°，

∴∠AFE=30°，

∴AE=，

∴EF＝2；

（2）如图，连接BD，DF，DF交PP′于H．

由题意PP′＝AA′＝AB＝CD，PP′∥AA′∥CD，

∴四边形PP′CD是平行四边形，

∵四边形ABCD是菱形，∠A＝60°，

∴△ABD是等边三角形，

∵AF＝FB，

∴DF⊥AB，DF⊥PP′，

在Rt△AEF中，∵∠AEF＝90°，∠A＝60°，AF＝4，

∴AE＝2，EF＝2，

∴PE＝PF＝，

在Rt△PHF中，∵∠FPH＝30°，PF＝，

∴HF＝PF＝，

∵DF＝=4，

∴DH＝4﹣＝，

∴平行四边形PP′CD的面积＝×8＝28．