Question

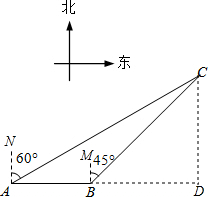
如图，大海中某岛C的周围25km范围内有暗礁．一艘海轮向正东方向航行，在A处望见C在北偏东60°处，前进20km后到达点B，测得C在北偏东45°处．如果该海轮继续向正东方向航行，有无触礁危险？请说明理由．
（参考数据：≈1.41，≈1.73）

Answer 1

解：该海轮继续向正东方向航行，无触礁危险．
理由：过点C作CD⊥AB于点D，
∴∠BCD=∠CBM=45°，
设BD=xkm，则CD==x（km），
∵∠CAN=60°，
∴∠CAD=30°，
在Rt△CAD中，tan∠CAB=tan30°==，
∴AD=CD=x（km），
∵AB=20km，AB+DB=AD，
∴20+x=x，
解得：x=10+10（km），
∴CD=10+10≈27.3（km）＞25km，
∴该海轮继续向正东方向航行，无触礁危险．
分析：判断有无危险只要求出点C到AB的距离，与6海里比较大小就可以．首先过点C作CD⊥AB于点D，设BD=xkm，由三角函数的定义，即可求得CD=xkm，AD=xkm，则可方程20+x=x，解此方程即可求得CD的长，比较即可求得答案．
点评：本题主要考查了方向角问题．此题难度适中，解题的关键是构造直角三角形，再解直角三角形，注意数形结合思想与方程思想的应用．