题目内容
在4×4的正方形网格中，每个小方形的边长都是1．线段AB、EA分别是图中1×3的两个长方形的对角线，请你证明AB⊥EA．
解：∵AE=
=
，AB==，BE=
，
∴AE2+AB2=BE2，
∴△ABE是直角三角形，
∴AB⊥EA．
分析：由勾股定理分别求得AE、AB、BE的值，再证明AE2+AB2=BE2，即可证明AB⊥EA．
点评：此题考查在网格中勾股定理和逆定理的应用，也是常用的方法．
=，AB==，BE=，∴AE2+AB2=BE2，
∴△ABE是直角三角形，
∴AB⊥EA．
分析：由勾股定理分别求得AE、AB、BE的值，再证明AE2+AB2=BE2，即可证明AB⊥EA．
点评：此题考查在网格中勾股定理和逆定理的应用，也是常用的方法．
练习册系列答案
相关题目
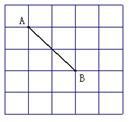
（2011•岳池县模拟）在6×8的正方形网格中建立了如图所示的平面直角坐标系xoy，已知每个最小正方形边长为1，将图中的OA绕O点逆时针旋转90°得到OA′，则A′点坐标为
如图，在10×10的正方形网格纸中（每个小方格的边长都是1个单位）有一个△ABC，请在网格纸中画出以点O为旋转中心把△ABC按顺时针方向旋转90°得到的△A′B′C′．