题目内容
已知四边形ABCD中,E、F分别是AB、AD边上的点,DE与CF交于点G.
(1)如图①,若四边形ABCD是矩形,且DE⊥CF,求证![]() ;
;
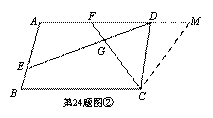
 (2)如图②,若四边形ABCD是平行四边形,试探究:当∠B与∠EGC满足什么关系时,使得
(2)如图②,若四边形ABCD是平行四边形,试探究:当∠B与∠EGC满足什么关系时,使得![]() 成立?并证明你的结论;
成立?并证明你的结论;

 (3)如图③,若BA=BC=6,DA=DC=8,∠BAD=90°,DE⊥CF,请直接写出
(3)如图③,若BA=BC=6,DA=DC=8,∠BAD=90°,DE⊥CF,请直接写出![]() 的值.
的值.
解:(1)选择二次函数,设![]() ,得
,得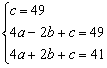 ,解得
,解得![]()
∴![]() 关于
关于![]() 的函数关系式是
的函数关系式是![]() .
.
不选另外两个函数的理由:
注意到点(0,49)不可能在任何反比例函数图象上,所以![]() 不是
不是![]() 的反比例函数;点(-4,41),(-2,49),(2,41)不在同一直线上,所以
的反比例函数;点(-4,41),(-2,49),(2,41)不在同一直线上,所以![]() 不是
不是![]() 的一次函数.
的一次函数.
(2)由(1),得![]() ,∴
,∴![]() ,
,
∵![]() ,∴当
,∴当![]() 时,
时,![]() 有最
有最![]() 大值为5
大值为5![]() 0.
0.
即当温度为-1℃时,这种植物每天高度增长量最大.
(3)![]() .
.
24.(本题满分10分)
(1)证明:∵四边形ABCD是矩形,∴∠A=∠ADC=90°,
∵DE⊥CF,∴∠ADE=∠DCF,∴△ADE∽△DCF,∴![]() .
.
(2)当∠B+∠EGC=180°时,![]() 成立,证明如下:
成立,证明如下: ![]()
在AD的延长线上取点M,使CM=CF,则∠CMF=∠CFM.
∵AB∥CD,∴∠A=∠CDM,
∵∠B+∠EGC=180°,
∴∠AED=∠FCB,∴∠CMF=∠AED.
∴△ADE∽△DCM,
∴![]() ,即
,即![]() .
.
(3)![]() .
.
 |

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
已知四边形ABCD中,给出下列四个论断:(1)AB∥CD,(2)AB=CD,(3)AD=BC,(4)AD∥BC.以其中两个论断作为条件,余下两个作为结论,可以构成一些命题.在这些命题中,正确命题的个数有( )
| A、2个 | B、3个 | C、4个 | D、6个 |
选做题:(A)已知四边形ABCD中,AD∥BC,对角线AC、BD交于点O,∠OBC=∠OCB,并且 ,求证:四边形ABCD是 形.(要求在已知条件中的横线上补上一个条件 ,在求证中的横线上添上该四边形的形状,然后画出图形,予以证明,证明时要用上所有条件)
(B)某市市委、市府2001年提出“工业立市”的口号,积极招商引资,财政收入稳步增长,各年度财政收入如下表:
按这种增长趋势,请你算一算2006年该市的财政收入是多少亿元.
(B)某市市委、市府2001年提出“工业立市”的口号,积极招商引资,财政收入稳步增长,各年度财政收入如下表:
| 年 份 | 2001 | 2002 | 2003 | 2004 | … |
| 财政收入 单位(亿元) |
10 | 10.5 | 12 | 14.5 | … |
 如图,已知四边形ABCD中,BC=CD=DB,∠ADB=90°,cos∠ABD=
如图,已知四边形ABCD中,BC=CD=DB,∠ADB=90°,cos∠ABD= 如图,已知四边形ABCD中,E、F、G、H分别为AB、BC、CD、DA的中点,
如图,已知四边形ABCD中,E、F、G、H分别为AB、BC、CD、DA的中点,