Question

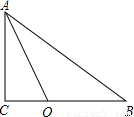
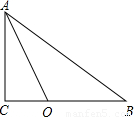
（2005•贵阳）在Rt△ABC中，∠C=90°，AC=6，BC=8，点O在CB上，且AO平分∠BAC，CO=3（如图所示），以点O为圆心，r为半径画圆．
（1）r取何值时，⊙O与AB相切；
（2）r取何值时，⊙O与AB有两个公共点；
（3）当⊙O与AB相切时，设切点为D，在BC上是否存在点P，使△APD的面积为△ABC的面积的一半？若存在，求出CP的长；若不存在，请说明理由．

Answer 1

【答案】分析：（1）⊙O与AB相切，则r等于圆的半径；
（2）⊙O与AB有两个公共点，则OA＞OB；
（3）连接OD，过点P做PH⊥AB于H，根据PH∥OD，，得到PH=（8-x），再根据S_△APD=S_△ABC，就可以求出PC的长．
解答：解：（1）过点D作DO⊥AB于D，
∵∠1=∠2，∠C=90°，
∴OD=OC=3，
故当r=3时，⊙O与AB相切；

（2）在Rt△AOC中，AO=，
而OB=BC-OC=8-3=5，
∴OA＞OB
∴当3＜r≤5时，⊙O与AB有两个公共点；

（3）连接OD，过点P做PH⊥AB于H；
设CP=x，则PB=8-x，
∵D为切点，
∴OD⊥AB，
∴PH∥OD，
∴，，
∴PH=（8-x），
∵AC⊥OC，
∴AC切⊙O于C，
∴AD=AC=6；
∴S_△APD=AD•PH=×6×（8-x）=-x；
由题意：S_△APD=S_△ABC
∴
∴；
故当PC=时，存在P点，使S_△APD=S_△ABC．
点评：本题主要考查了直线与圆的位置关系的判定方法，可以利用比较半径与圆心到直线的距离来比较得到．