题目内容
(1)计算:cos60°+sin245°-tan30°•tan45°;
(2)在Rt△ABC中,∠ACB=90°,CD⊥AB于D,AB=2BC,求cos∠ACD的值.
解:(1)原式= +(
+( )2-
)2- ×1
×1
= +
+ -
-
=1- ;
;
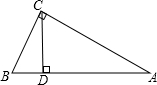
(2)∵∠ACB=90°,AB=2BC,
∴∠A=30°,
∵CD⊥AB,∴∠ACD=60°,
∴cos∠ACD=cos60°= .
.
分析:(1)利用特殊角的三角函数值得出原式各项中三角函数的值,化简后即可求出值;
(2)根据题意画出相应的图形,由斜边AB等于直角边BC的2倍,可得出BC所对的角为30°,即角A为30°,由CD垂直于AB,得到三角形ACD为直角三角形,根据直角三角形中两锐角互余可得出∠ACD的度数,利用特殊角的三角函数值即可求出cos∠ACD的值.
点评:此题考查了特殊角的三角函数值,在直角三角形中若一直角边等于斜边的一半,可得出这条直角边所对的角为30°,以及锐角三角函数定义,牢记特殊角的三角函数值是解本题第一问的关键.
 +(
+( )2-
)2- ×1
×1=
 +
+ -
-
=1-
 ;
;
(2)∵∠ACB=90°,AB=2BC,
∴∠A=30°,
∵CD⊥AB,∴∠ACD=60°,
∴cos∠ACD=cos60°=
 .
.分析:(1)利用特殊角的三角函数值得出原式各项中三角函数的值,化简后即可求出值;
(2)根据题意画出相应的图形,由斜边AB等于直角边BC的2倍,可得出BC所对的角为30°,即角A为30°,由CD垂直于AB,得到三角形ACD为直角三角形,根据直角三角形中两锐角互余可得出∠ACD的度数,利用特殊角的三角函数值即可求出cos∠ACD的值.
点评:此题考查了特殊角的三角函数值,在直角三角形中若一直角边等于斜边的一半,可得出这条直角边所对的角为30°,以及锐角三角函数定义,牢记特殊角的三角函数值是解本题第一问的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
