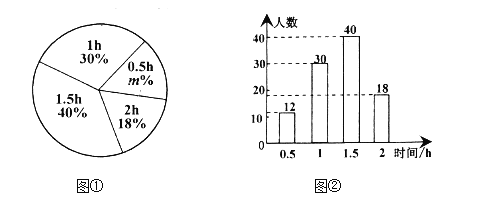
题目内容
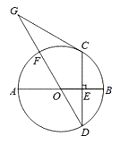
【题目】如图,在 RtABC 中,ACB 90 ,点 E 为 AB 中点,经过 A 、C 、E 三点的⊙O 与 BC的延长线相交于点 D ,过点 D 的直线交 AB 的延长线于点 F ,且FDB CED 。
(1)求证: DF 为⊙O 的切线;
(2)若 AE ![]() ,CD 1,求 DF ;
,CD 1,求 DF ;
(3)若 BF mBE ,求sin BAC (用含 m 的代数式表示).
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
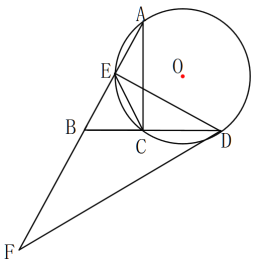
(1)连接AD,由圆周角定理可得到∠CED=∠CAD,进而证得∠CAD=∠FDB, ∠ADF=90°,所以得到DF 为⊙O 的切线;
(2)先证得AD=BD,再设BC=x,则BD=1+x=AD,根据勾股定理列出![]() 解得x=3, AD=4,再求得
解得x=3, AD=4,再求得![]() ,再证得∠ADE=∠F并根据它们的正切值相等列出方程,
,再证得∠ADE=∠F并根据它们的正切值相等列出方程,![]() 即可求出DF;
即可求出DF;
(3)设BE=a,则BF=ma,AE=a,AF=(m+2)a,EF=(m+1)a,由射影定理可证![]() ,
,![]() ,
,![]() ,再证得∠ADE=∠BDE=∠BAC=∠F,则
,再证得∠ADE=∠BDE=∠BAC=∠F,则![]()
(1)连接AD
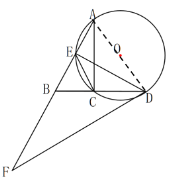
∵∠ACD=90°,
∴∠CAD+∠ADC=90°,AD是直径.
∵∠CED=∠CAD, ∠CED=∠FDB,
∴∠CAD=∠FDB,
∴∠ADC+∠FDB=90°,即∠ADF=90°,
∴DF 为⊙O 的切线;
(2) ∵∠ACD=90°,
∴AD是直径,
∴DE⊥AB,
∵点 E 为 AB 中点,
∴DE是AB的中垂线,
∴AD=BD
设BC=x,则BD=1+x=AD,
在Rt△ABC中,![]()
Rt△ACD中,![]()
∴![]()
解得![]() (舍去),
(舍去),
∴AD=4
在Rt△ADE中,![]() ,
,
由已知易证∠ADE=∠F
∴![]()
![]()
∴![]()
![]()
(3)设BE=a,则BF=ma,
AE=a,AF=(m+2)a,EF=(m+1)a
在Rt△ADF中,由射影定理可证![]()
![]()
![]()

∵∠ADF=90°,DE垂直平分AB, ∠ACD=90°,
∴∠ADE=∠BDE=∠BAC=∠F,
∴![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案