题目内容
【题目】如图,![]() 内接于
内接于![]() ,
,![]() 的延长线交
的延长线交![]() 于点
于点![]() .
.

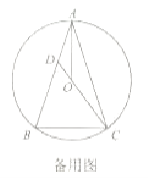
(1)求证![]() 平分
平分![]() ;
;
(2)若![]() ,求
,求![]() 和
和![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]() ;
;![]() .
.
【解析】
试题分析:(1)连接OB,证明ΔAOB≌ΔAOC即可得出结论;
(2)过点C作CE⊥AB于E,由sin∠BAC=![]() ,设AC=5m,CE=3则可表示出AE=4m,BE=m,在RtΔCBE中,由勾股定理可求出m的值,即可得出AC的值;延长AO交BC于点H,则AH⊥BC,过点O作OF⊥AH,可求OF的值,由OF∥BC可得结论.
,设AC=5m,CE=3则可表示出AE=4m,BE=m,在RtΔCBE中,由勾股定理可求出m的值,即可得出AC的值;延长AO交BC于点H,则AH⊥BC,过点O作OF⊥AH,可求OF的值,由OF∥BC可得结论.
试题解析:(1)证明:连接OB
∵AO=AO,BO=CO,AB=AC
∴ΔAOB≌ΔAOC
∴∠BAO=∠CAO
即AO平分∠BAC
(2)过点C作CE⊥AB于E
∵sin∠BAC=![]() ,设AC=5m,则CE=3m
,设AC=5m,则CE=3m
∴AE=4m,BE=m
在RtΔCBE中,m2+(3m)2=36
∴m=![]() ,
,
∴AC=![]()
延长AO交BC于点H,则AH⊥BC,且BH=CH=3,
过点O作OF⊥AH交AB于点F,

∵∠HOC=∠BAC
∴OH=4,OC=5
∴AH=9
∴tan∠BAH=![]()
∴OF=![]() AO=
AO=![]()
∵OF∥BC
∴![]() ,即
,即
∴DC=![]() .
.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目





