题目内容
 一条公路弯道处是一段圆弧
一条公路弯道处是一段圆弧 |
| AB |
 |
| AB |
100m
100m
.分析:先连接OA,由垂径定理求出AD的长,再设OA=r,在Rt△AOD中,利用勾股定理列出方程,求出r的长,即可求出答案.
解答:解:连接OA,
∵C是
的中点,OC与AB相交于点D,
∴AB⊥OC,
∴AD=
AB
∵AB=120m,
∴AD=
×120=60m,
设OA=r,则OD=OC-CD=r-CD,
∵CD=20m,
∴OD=r-20m,
在Rt△AOD中,
∵OA2=AD2+OD2,
∴r2=602+(r-20)2,
解得r=100m.
故答案为:100m.

∵C是
 |
| AB |
∴AB⊥OC,
∴AD=
| 1 |
| 2 |
∵AB=120m,
∴AD=
| 1 |
| 2 |
设OA=r,则OD=OC-CD=r-CD,
∵CD=20m,
∴OD=r-20m,
在Rt△AOD中,
∵OA2=AD2+OD2,
∴r2=602+(r-20)2,
解得r=100m.
故答案为:100m.
点评:此题考查了垂径定理的应用,用到的知识点是垂径定理、勾股定理,关键是根据定理列出方程,是一道典型题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
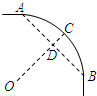 (2011•南宁)一条公路弯道处是一段圆弧
(2011•南宁)一条公路弯道处是一段圆弧 ,点O是这条弧所在圆的圆心,点C是
,点O是这条弧所在圆的圆心,点C是 的中点,OC与AB相交于点D.已知AB=120m,CD=20m,那么这段弯道的半径为 .
的中点,OC与AB相交于点D.已知AB=120m,CD=20m,那么这段弯道的半径为 .
 ,点O是这条弧所在圆的圆心,点C是
,点O是这条弧所在圆的圆心,点C是 的中点,OC与AB相交于点D.已知AB=120m,CD=20m,那么这段弯道的半径为( )
的中点,OC与AB相交于点D.已知AB=120m,CD=20m,那么这段弯道的半径为( )
 m
m m
m ,点O是这条弧所在圆的圆心,点C是
,点O是这条弧所在圆的圆心,点C是 的中点,OC与AB相交于点D.已知AB=120m,CD=20m,那么这段弯道的半径为( )
的中点,OC与AB相交于点D.已知AB=120m,CD=20m,那么这段弯道的半径为( )
 m
m m
m