题目内容
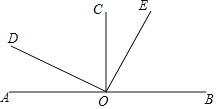
如图,已知直线AB上一点O,OC⊥AB,OD⊥OE, 若∠COE= ∠BOD.
∠BOD.
(1)求∠COE, ∠BOD, ∠AOE的度数.
(2)若OF平分∠BOE,求∠AOF的度数.
练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
题目内容
如图,已知直线AB上一点O,OC⊥AB,OD⊥OE, 若∠COE= ∠BOD.
∠BOD.
(1)求∠COE, ∠BOD, ∠AOE的度数.
(2)若OF平分∠BOE,求∠AOF的度数.

 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案