Question

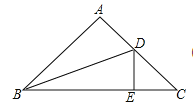
【题目】如图，在ΔABC中，∠A=90°，∠C=45°，BC=8，∠ABC的角平分线交AC于点D，DE⊥BC，则CΔDEC=___________。

Answer 1

【答案】8．

【解析】

由已知ΔABC中，∠A=90°，∠C=45°可得AB=AC，根据角平分线上的点到角的两边距离相等可得ED=AD，利用“HL”证明Rt△ABD和Rt△EBD全等，根据全等三角形对应边相等可得AB=EB，然后求出△DEC的周长=BC，再根据BC=8，即可得出答案．

解：∵ΔABC中，∠A=90°，∠C=45°，

∴AB=AC，

∵BD是∠ABC的平分线，DE⊥BC，∠A=90°，
∴DE=AD，
在Rt△ABD和Rt△EBD中，
∵ ，
∴Rt△ABD≌Rt△EBD（HL），
∴AB=EB，
∴△DEC的周长=DE+CD+CE
=AD+CD+CE，
=AC+CE，
=AB+CE，
=BE+CE，
=BC，
∵BC=8，
∴CΔDEC=8．
故答案为：8．