题目内容
如图，在平行四边形ABCD中，E为CD上一点，DE：CE=2：3，连结AE、BD，且AE、BD交于点F，则S△DEF：S△BAF等于（ ）| A、4：25 | B、4：9 |
| C、2：3 | D、2：5 |
考点：相似三角形的判定与性质,平行四边形的性质
专题：
分析：根据已知可得到相似三角形，从而可得到其相似比，再根据相似三角形的面积比等于相似比的平方就可得到答案．
解答：解：如图，∵四边形ABCD是平行四边形，
∴DC∥AB，CD=AB．
∴△DFE∽△BFA，
∴S△DEF：S△BAF=DE2：AB2．
∵DE：EC=2：3，
∴DE：DC=DE：AB=2：5，
∴S△DEF：S△ABF=4：25
故选：A．
∴DC∥AB，CD=AB．
∴△DFE∽△BFA，
∴S△DEF：S△BAF=DE2：AB2．
∵DE：EC=2：3，
∴DE：DC=DE：AB=2：5，
∴S△DEF：S△ABF=4：25
故选：A．
点评：本题考查的是相似三角形的判定与性质及平行四边形的性质，熟知相似三角形边长的比等于相似比，面积的比等于相似比的平方是解答此题的关键．
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
导学与测试系列答案
相关题目
如图是正方体的平面展开图，每个面上都标有一个汉字，与“五”字对应的面上的字为（ ）| A、我 | B、爱 | C、中 | D、学 |
式子
+
有意义，则字母a的取值范围是（ ）
| 7-a |
| a-5 |
| A、a≥5 | B、a≤7 |
| C、a≥5或a≤7 | D、5≤a≤7 |
下列方程是一元一次方程的是（ ）
A、
| ||
| B、x=3 | ||
| C、x2-l=0 | ||
| D、3x+2y=0 |
根据锐角三角函数的定义，填写下面的图表：
小刚、小明用图中两个可自由转动的转盘做“配紫色”游戏：分别旋转两个转盘，若其中一个转出红色，另一个转出蓝色即可配成紫色，此时小刚得1分，否则小明得1分．这个游戏对双方公平吗？
如图，已知线段AB，在方格纸上画出以下图形：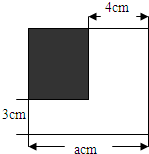
如图，一块正方形铁皮的边长为a厘米，若一边截去4厘米，另一边截去3厘米．