题目内容
【题目】如图,是将抛物线 ![]() 平移后得到的抛物线,其对称轴为
平移后得到的抛物线,其对称轴为 ![]() ,与x轴的一个交点为A
,与x轴的一个交点为A ![]() ,另一交点为B,与y轴交点为C.
,另一交点为B,与y轴交点为C.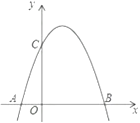
(1)求抛物线的函数表达式;
(2)若点 ![]() 为抛物线上一点,且BC⊥NC,求点N的坐标;
为抛物线上一点,且BC⊥NC,求点N的坐标;
(3)点P是抛物线上一点,点Q是一次函数 ![]() 的图象上一点,若四边形OAPQ为平行四边形,这样的点P、Q是否存在?若存在,分别求出点P、Q的坐标,若不存在,说明理由.
的图象上一点,若四边形OAPQ为平行四边形,这样的点P、Q是否存在?若存在,分别求出点P、Q的坐标,若不存在,说明理由.
【答案】
(1)解:设抛物线的解析式是 ![]() .
.
把 ![]() 代入得
代入得 ![]() ,解得,
,解得, ![]()
则抛物线的解析式是 ![]() ,即
,即 ![]() ;
;
(2)解:
方法一:设直线BC的解析式为 ![]() ,
,
![]()
∴直线BC的解析式为 ![]() ,
,
由BC⊥NC,则设直线CN的解析式为 ![]()
![]() ,即直线CN的解析式为
,即直线CN的解析式为 ![]()
∵N为直线BC与CN的交点,
∴联立方程得: ![]() ,即
,即 ![]() ,
,
∴ ![]() ,则N的坐标是
,则N的坐标是 ![]()
方法二:在 ![]() 中令
中令 ![]() ,则
,则 ![]() ,
,
即C的坐标是 ![]() ,OC=3.
,OC=3.
∵B的坐标是 ![]() ,
,
∴OB=3,
∴OC=OB,则△OBC是等腰直角三角形.
∴∠OCB=45°,
过点N作NH⊥y轴,垂足是H.
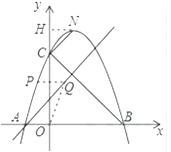
∵∠NCB=90°,∴∠NCH=45°,
∴NH=CH,∴HO=OC+CH=3+CH=3+NH,
设点N纵坐标是 ![]() .
.
∴ ![]() ,
,
解得 ![]() (舍去)或
(舍去)或 ![]() ,
,
∴N的坐标 ![]() ;
;
(3)解:∵四边形OAPQ是平行四边形,
则PQ=OA=1,且PQ∥OA,
设 ![]() ,则
,则 ![]() 代入
代入 ![]() ,
,
得 ![]() ,
,
整理,得 ![]() ,
,
解得 ![]() 或
或 ![]() .
.
∴ ![]() 的值为3或
的值为3或 ![]() .
.
∴P、Q的坐标是 ![]() 或
或 ![]() .
.
【解析】(1)由其对称轴为 x = 1 ,可得顶点横坐标为1,再由与x轴的一个交点为A ( 1 , 0 ),且由平移可得a=-1,所以易由顶点式求得解析式为y = x 2 + 2 x + 3
(2)由B(3,0)C(0,3)易得直线BC为y = x + 3 ,由于BC⊥NC,可得直线NC的斜率k=1,结合点C(0,3),可得到直线NC为y = x + 3;所求点N为二次函数与直线NC的交点,连列方程组可得N的坐标是 ( 1 , 4 )。
(3)由四边形OAPQ是平行四边形易得PQ=OA=1,且PQ∥OA,所以若设 P ( t , t 2 + 2 t + 3 ),则可得 Q ( t + 1 , t 2 + 2 t + 3 )由于Q为直线y = ![]() x +
x + ![]() 的点,代入可计算出t= 0 或 t =
的点,代入可计算出t= 0 或 t = ![]() ,代入所设 P ( t , t 2 + 2 t + 3 ), Q ( t + 1 , t 2 + 2 t + 3 ) 即可得两点坐标。
,代入所设 P ( t , t 2 + 2 t + 3 ), Q ( t + 1 , t 2 + 2 t + 3 ) 即可得两点坐标。
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点,以及对二次函数的性质的理解,了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案


