题目内容
【题目】如图，二次函数
的图像与
轴交于点A
、B
，与
轴交于点C．
（1）
； 
；
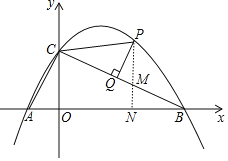
（2）点P为该函数在第一象限内的图像上的一点，过点P作
于点Q，连接PC，
①求线段PQ的最大值；
②若以P、C、Q为顶点的三角形与
相似，求点P的坐标．
【答案】（1）
；
（2）①PQ的最大值是
；②P的坐标为
或
【解析】试题分析：（1）设交点式y=a（x+1）（x-4），再展开可得到-4a=2，解得a=-
，即可得到b的值；
（2）①作PN⊥x轴于N，交BC于M，如图，先利用待定系数法求出直线BC的解析式为y=-
x+2，设P（t，-
t2+
t+2），则M（t，-
t+2），用t表示出PM=-
t2+2t，再证明△PQM∽△BOC，利用相似比得到PQ=-
t2+
t，然后利用二次函数的性质解决问题；②讨论：当∠PCQ=∠OBC时，△PCQ∽△CBO，PC∥x轴，利用对称性可确定此时P点坐标；当∠CPQ=∠OBC时，△CPQ∽△CBO，则∠CPQ=∠MPQ，所以△PCM为等腰三角形，则PC=PM，利用两点间的距离公式得到t2+（-
t2+
t+2-2）2=（-
t2+2t）2，然后解方程求出t得到此时P点坐标．
试题解析：（1）设抛物线解析式为y=a(x+1)(x4)，
即y=ax23ax4a，
则4a=2,解得a=
，
则b=-3a=
；
（2）(2)①作PN⊥x轴于N，交BC于M，如图，
BC=
，
当x=0时，y=-
x2+
x+2=2，则C(0，2)，
设直线BC的解析式为y=mx+n，
把C(0，2)，B(4，0)得
，解得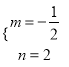
，
∴直线BC的解析式为y=
x+2，
设P(t， 
t2+
t+2)，则M(t， 
t+2)，
∴PM=
t2+
t+2(
t+2)= 
t2+2t，
∵∠NBM=∠NPQ，
∴△PQM∽△BOC，
∴
，即PQ=
，
∴PQ=
t2+
t=
(t2)2+
，
∴当t=2时，线段PQ的最大值为
；
②当∠PCQ=∠OBC时,△PCQ∽△CBO，
此时PC∥OB,点P和点C关于直线x=
对称，
∴此时P点坐标为(3，2)；
当∠CPQ=∠OBC时，△CPQ∽△CBO，
∵∠OBC=∠NPQ，
∴∠CPQ=∠MPQ，
而PQ⊥CM，
∴△PCM为等腰三角形，
∴PC=PM，
∴t2+(
t2+
t+22)2=(
t2+2t)2，
解得t=
，
此时P点坐标为(
， 
)，
综上所述,满足条件的P点坐标为(3，2)或(
， 
).
