题目内容
【题目】在平面直角坐标系中，直线
与
轴、
轴分别交于点B、 A，点D、E分别是AO、AB的中点，连接DE，点P从点D出发，沿DE方向匀速运动，速度为1cm/s；与此同时，点Q从点B出发，沿BA方向匀速运动，速度为2cm/s，当点P停止运动时，点Q也停止运动．连接PQ，设运动时间为
.
（1）分别写出点P和Q坐标（用含t的代数式表示）；
（2）①当点Q在BE之间运动时，设五边形PQBOD的面积为
（cm2），求y与t之间的函数关系式；
②在①的情况下，是否存在某一时刻t，使PQ分四边形BODE两部分的面积之比为S△PQE：S五边形PQBOD＝1：29？若存在，求出此时t的值；若不存在，请说明理由；
（3）以P为圆心、PQ长为半径作圆，请问：在整个运动过程中，当t为何值时，⊙P能与△ABO的一边相切？
【答案】（1）P(t，3)，Q(8－
t， 
t)；
（2）①
②t＝2，理由见解析
（3）当t＝
， 
， 
时，⊙P可与△ABC的一边相切.
【解析】试题分析：（1）利用直线的解析式首先求得直线与两坐标轴的交点坐标，然后利用三角形的中位线定理求得点P的纵坐标和点P的横坐标即可；（2）①由P作PH⊥AB得到△PHE∽△AOB，利用相似三角形对应边的比相等表示出PH，然后根据三角形的面积公式求解即可；②利用S△PQE：S五边形PQBOD＝1：29列出方程求得t值即可;（3）分当⊙P与OB相切时、当⊙P与OA相切时和当⊙P与AB相切时三种情况分类讨论得到答案．
试题解析：
（1）P(t，3)，Q(8－
t， 
t)；
（2）
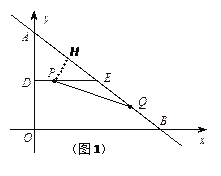
①如图1，P做PH⊥AB
△PHE∽△AOB
∴
∴
S△PEQ =
S四边形DOBE＝
×3＝18
②
×18 解得t＝－
（舍），t＝2
（3）
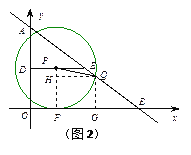
当⊙P与OB相切时，分别过点P、Q作PF、QG垂直于x轴，垂足为F、G，再过点Q作QH⊥PF于点H，如图2构造直角△PHQ，
此时，△BQG∽△BAO，BQ＝2t，得QG＝HF＝
t，BG＝
t，
在Rt△PHQ中，PH2＋HQ2＝PQ2，得(3－
t)2＋(8－t－
t)2＝32，
解得： t1＝4(舍)，t2＝
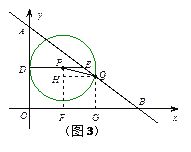
当⊙P与OA相切时，分别过点P、Q作PF、QG垂直于x轴，垂足为F、G，再过点Q作QH⊥PF于点H，如图3构造直角△PHQ，此时，△BQG∽△BAO，BQ＝2t，得QG＝HF＝
t，BG＝
t，
在Rt△PHQ中，PH2＋HQ2＝PQ2，得(3－
t)2＋(8－t－
t)2＝t2，
解得： t1＝
＞4(舍)，t2＝
当⊙P与AB相切时，如图4，此时， PE＝4－t，EQ＝2t－5，
由△EPQ∽△BAO，得
，∴
，解得： t＝
∴当t＝
， 
， 
时，⊙P可与△ABC的一边相切．
