题目内容
如图,等边三角形 放在平面直角坐标系中,其中点
放在平面直角坐标系中,其中点 为坐标原点,点
为坐标原点,点 的坐标为(
的坐标为( ,
, ),点
),点 位于第二象限.已知点
位于第二象限.已知点 、点
、点 同时从坐标原点出发,点
同时从坐标原点出发,点 以每秒
以每秒 个单位长度的速度沿
个单位长度的速度沿 来回运动一次,点
来回运动一次,点 以每秒
以每秒 个单位长度的速度从
个单位长度的速度从 往
往 运动,当点
运动,当点 到达点
到达点 时,
时, 、
、 两点都停止运动.在点
两点都停止运动.在点 、点
、点 的运动过程中,存在某个时刻,使得
的运动过程中,存在某个时刻,使得 、
、 两点与点
两点与点 或点
或点 构成的三角形为直角三角形,那么点
构成的三角形为直角三角形,那么点 的坐标为__________.
的坐标为__________.

【答案】
( ,
, )、(
)、( ,
, )、(
)、( ,
, )、(
)、( ,
, )
)
【解析】解:因为等边三角形 放在平面直角坐标系中,点
放在平面直角坐标系中,点 的坐标为(
的坐标为( ,
, ),点
),点 位于第二象限就,其为(-4,4
位于第二象限就,其为(-4,4 ),那么根据点的坐标,以及它们两个点运行的速度比为4:1,可知,使得
),那么根据点的坐标,以及它们两个点运行的速度比为4:1,可知,使得 、
、 两点与点
两点与点 或点
或点 构成的三角形为直角三角形的情况共有4种,并且此时点P的坐标为(
构成的三角形为直角三角形的情况共有4种,并且此时点P的坐标为( ,
, )、(
)、( ,
, )、(
)、( ,
, )、(
)、( ,
, )
)

练习册系列答案
相关题目
 已知,如图,等边三角形ABC边长为2,以BC为对称轴将△ABC翻折,得到四边形ABDC,将此四边形放在直角坐标系xOy中,使AB在x轴上,点D在直线
已知,如图,等边三角形ABC边长为2,以BC为对称轴将△ABC翻折,得到四边形ABDC,将此四边形放在直角坐标系xOy中,使AB在x轴上,点D在直线 放在平面直角坐标系中,其中点
放在平面直角坐标系中,其中点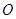 为坐标原点,点
为坐标原点,点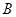 的坐标为(
的坐标为( ,
, ),点
),点 位于第二象限.已知点
位于第二象限.已知点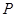 、点
、点 同时从坐标原点出发,点
同时从坐标原点出发,点 个单位长度的速度沿
个单位长度的速度沿 来回运动一次,点
来回运动一次,点 个单位长度的速度从
个单位长度的速度从
 上.
上. 与y轴交于点P,抛物线y=ax2+bx+c,过A、B、P三点,求这条抛物线的函数关系式;
与y轴交于点P,抛物线y=ax2+bx+c,过A、B、P三点,求这条抛物线的函数关系式;
 上.
上. 与y轴交于点P,抛物线y=ax2+bx+c,过A、B、P三点,求这条抛物线的函数关系式;
与y轴交于点P,抛物线y=ax2+bx+c,过A、B、P三点,求这条抛物线的函数关系式;